题目内容
【题目】如图,用长为![]() 的铝合金条制成“日”字形窗框,若窗框的宽为
的铝合金条制成“日”字形窗框,若窗框的宽为![]() ,窗户的透光面积为
,窗户的透光面积为![]() (铝合金条的宽度不计).
(铝合金条的宽度不计).

(Ⅰ)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(Ⅱ)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
【答案】(Ⅰ)y=﹣![]() (0<x<2),(Ⅱ)当x=1时,y最大=
(0<x<2),(Ⅱ)当x=1时,y最大=![]() m2,
m2,
【解析】对于(1),根据题意可知长为![]() m,结合长方形的面积公式,即可得到y与x的函数关系式,注意x的取值范围;
m,结合长方形的面积公式,即可得到y与x的函数关系式,注意x的取值范围;
对于(2),根据(1)中结论可知y与x是二次函数关系,根据二次函数的性质即可求得最大面积;
本题解析:
(1)∵大长方形的周长为6m,宽为xm,
∴长为![]() m,
m,
∴y=x![]() =﹣
=﹣![]() (0<x<2),
(0<x<2),
(2)由(1)可知:y和x是二次函数关系,
a=﹣![]() <0,
<0,
∴函数有最大值,
当x=﹣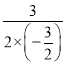 =1时,y最大=
=1时,y最大=![]() m2,
m2,
答:窗框的长和宽分别为1.5m和1m时才能使得窗户的透光面积最大,此时的最大面积为1.5 m.

练习册系列答案
相关题目