题目内容
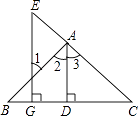
【题目】如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F,求证:PE﹣PF=CD. 
【答案】证明:过C作CG⊥PE于G, ∵PE⊥AB,CD⊥AB,CG⊥PE,
∴四边形CDEG是矩形,
∴CD=EG,
∵PF⊥AC,
∴∠PFC=90°,
∵CG⊥PE,
∴∠PGC=90°,
∴∠PFC=∠PGC,
∵AB=AC,
∴∠ABC=∠ACB,
∵CG⊥PE,AB⊥PE,
∴CG∥AB,
∴∠ABC=∠PCG,
又∵∠ACB=∠PCF(对顶角相等),
∴∠PCG=∠PCF,
在△PCG和△PCF中, ,
,
∴△PCG≌△PCF(AAS),
∴PF=PG,
∴PE﹣PG=PE﹣PF=EG=CD,
则PE﹣PF=CD.
【解析】过C作CG⊥PE于G,由三个角为直角的四边形为矩形得到CDEG为矩形,得到CD=EG,由一对直角相等,一对对顶角相等,且AC=AC,利用AAS得到三角形PCG与三角形PCF全等,利用全等三角形边相等得到PF=PG,由PE﹣PG=PE﹣PF=EG=CD,即可得证.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

练习册系列答案
相关题目