题目内容
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1 , 再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2 , 如此进行下去,得到四边形AnBnCnDn . 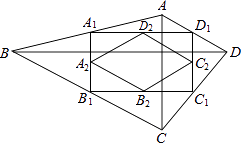
(1)求证:四边形A1B1C1D1是矩形;
(2)四边形A3B3C3D3是形;
(3)四边形A1B1C1D1的周长为;
(4)四边形AnBnCnDn的面积为 .
【答案】
(1)证明:∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,
∴四边形A1B1C1D1是矩形
(2)矩
(3)a+b
(4)![]()
【解析】(2)解:∵四边形A1B1C1D1是矩形, ∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
∴四边形A3B3C3D3是矩形,
所以答案是:矩; (3)解:根据三角形中位线定理可得D1C1=A1B1= ![]() AC=
AC= ![]() a,A1D1=B1C1=
a,A1D1=B1C1= ![]() BC=
BC= ![]() b.故四边形A1B1C1D1是的周长为a+b,
b.故四边形A1B1C1D1是的周长为a+b,
所以答案是:a+b.(4)解:∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是 ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目