题目内容
【题目】综合题。
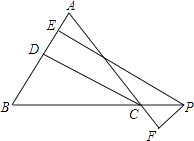
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:CN∥AB.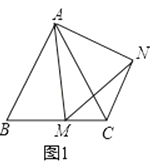
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论CN∥AB还成立吗?请说明理由.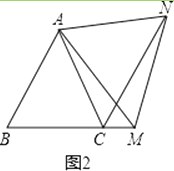
【答案】
(1)
证明:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM+∠MAC=∠MAC+∠CAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中, 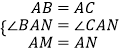
∴△ABM≌△ACN(SAS),
∴∠ACN=∠ABM=60°,
∵∠ACB=60°
∴∠BCN+∠ABM=180°;
∴CN∥AB
(2)
证明:成立,
理由如下:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠CAM=∠CAM+∠MAN,
∴∠BAM=∠CAN
在△ABM和△ACN中, 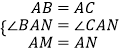 ,
,
∴△ABM≌△ACN(SAS),
∴∠ACN=∠ABM=60°,
∵∠ACB=60°
∴∠BCN+∠ABM=180°;
∴CN∥AB
【解析】(1)利用等边三角形的性质得出AB=AC,AM=AN,∠BAC=∠MAN,进而得出∠BAM=∠CAN,即可判断出△ABM≌△ACN(SAS),得出∠ACN=∠ABM=60°,进而得出∠BCN+∠ABM=180°即可得出结论;(2)同(1)的方法即可得出结论.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.

 寒假学与练系列答案
寒假学与练系列答案【题目】某服装店以每件82元的价格购进了30套保暖内衣,销售时,针对不同的顾客,这30套保暖内衣的售价不完全相同,若以100元为标准,将超过的钱数记为正,不足的钱数记为负,则记录结果如表所示:
售出件数 | 7 | 6 | 7 | 8 | 2 |
售价(元) | +5 | +1 | 0 | ﹣2 | ﹣5 |
请你求出该服装店在售完这30套保暖内衣后,共赚了多少钱?