题目内容
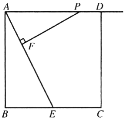
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
【答案】(1)当t=1或t=![]() 时,△BPQ与△ABC相似;(2)t=
时,△BPQ与△ABC相似;(2)t=![]() .
.
【解析】
试题(1)分两种情况:①当△BPQ∽△BAC时,BP:BA=BQ:BC;当△BPQ∽△BCA时,BP:BC=BQ:BA,再根据BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8-4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
试题解析:根据勾股定理得:BA=![]() =10;
=10;
(1)分两种情况讨论:
①当△BPQ∽△BAC时,![]()
∵BP=5t,QC=4t,AB=10,BC=8,
∴![]() ,解得,t=1,
,解得,t=1,
②当△BPQ∽△BCA时,![]()
∴![]() ,解得,t=
,解得,t=![]() ;
;
∴t=1或![]() 时,△BPQ∽△BCA;
时,△BPQ∽△BCA;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图所示:
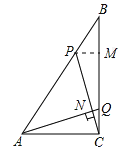
则PB=5t,PM=3t,MC=8-4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴![]()
∴![]() ,解得t=
,解得t=![]() .
.

练习册系列答案
相关题目