��Ŀ����
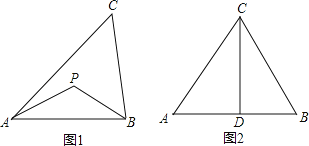
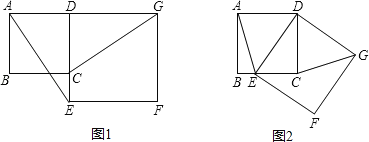
����Ŀ����ͼ1����֪������ABCD�ı�CD��������DEFG�ı�DE�ϣ�����AE��GC��
(1)�Բ���AE��GC�������Ĺ�ϵ(ֱ��д�����ۼ���)��
(2)��������DEFG�Ƶ�D��˳ʱ�뷽����ת��ʹ��E����BC���ϣ���ͼ2������AE��CG������Ϊ(1)�еĽ����Ƿ�����������������֤����������������˵�����ɣ�
(3)��(2)�У���E��BC���е㣬��BC��2����C��F�����ľ���Ϊ�� ����
���𰸡�(1) AE��CG��AE��GC��(2)������֤���������� (3)![]() ��
��
��������
��1���۲�ͼ�Σ�AE��CG��λ�ù�ϵ�����Ǵ�ֱ����������֤���������ı���ABCD��DEFG���������Σ���֤����ADE�ա�CDG�����1����2�����ڡ�2����3���࣬���ԡ�1����3���࣬�ɴ˿ɵ�AE��GC��
��2���⣨1���Ľ�����Ȼ���������գ�1����Ľ��ⷽ������֤��ADE�ա�CDG���á�5����4�����ڡ�4����7���࣬����5����6���࣬��ô��6����7����ͼ֪��AEB����CEH��90������6������7+��CEH��90�����ɴ˵�֤��
��3����ͼ3�У���CM��DG��G��GN��CD��N��CH��FG��H�����ı���CMGH�Ǿ��Σ��ɵ�CM��GH��CH��GM����취���CH��HF�������ù��ɶ������ɽ�����⣮
(1)AE��CG��AE��GC��
֤�����ӳ�GC��AE�ڵ�H��
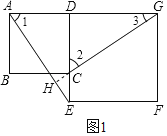
��������ABCD��������DEFG��
AD��DC����ADE����CDG��90����
DE��DG��
���ADE�ա�CDG(SAS)��
��AE��CG����1����2
�ߡ�2+��3��90����
���1+��3��90����
���AHG��180����(��1+��3)��180����90����90����
��AE��GC��
(2)�𣺳�����
֤�����ӳ�AE��GC�ཻ�ڵ�H��
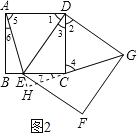
��������ABCD��������DEFG��
AD��DC��DE��DG����ADC����DCB����B����BAD����EDG��90����
���1����2��90������3��
���ADE�ա�CDG(SAS)��
��AE��CG����5����4��
�֡ߡ�5+��6��90������4+��7��180������DCE��180����90����90����
���6����7��
�֡ߡ�6+��AEB��90������AEB����CEH��
���CEH+��7��90����
���EHC��90����
��AE��GC��
(3)��ͼ3�У���CM��DG��G��GN��CD��N��CH��FG��H�����ı���CMGH�Ǿ��Σ��ɵ�CM��GH��CH��GM��
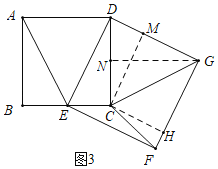
��BE��CE��1��AB��CD��2��
��AE��DE��CG�TDG��FG��![]() ��
��
��DE��DG����DCE����GND����EDC����DGN��
���DCE�ա�GND(AAS)��
��GCD��2��
��S��DCG��![]() CDNG��
CDNG��![]() DGCM��
DGCM��
��2��2��![]() CM��
CM��
��CM��GH��![]() ��
��
��MG��CH��![]() ��
��![]() ��
��
��FH��FG��FG��![]() ��
��
��CF��![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��