题目内容
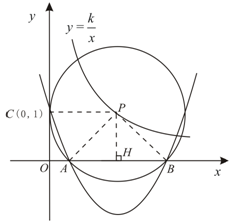
已知圆P的圆心在反比例函数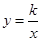
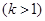 图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
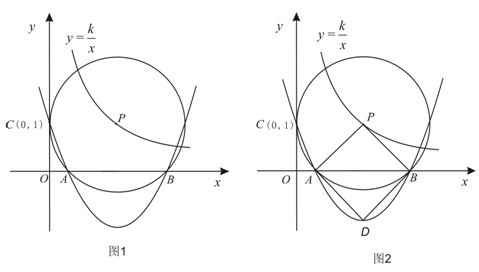
(1)求经过A、B、C三点的二次函数图象的解析式;
(2)若二次函数图象的顶点为D,问当k为何值时,四边形ADBP为菱形.
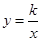
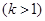 图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
(1)求经过A、B、C三点的二次函数图象的解析式;
(2)若二次函数图象的顶点为D,问当k为何值时,四边形ADBP为菱形.
(1) y=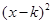 +1-
+1-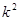 (2)
(2)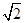
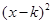 +1-
+1-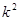 (2)
(2)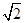
解:(1)连结PC、PA、PB,过P点作PH⊥x轴,垂足为H. …………………1分
∵⊙P与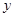 轴相切于点C (0,1),
轴相切于点C (0,1),
∴PC⊥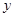 轴.
轴.
∵P点在反比例函数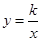 的图象上,
的图象上,
∴P点坐标为(k,1). …………………2分
∴PA=PC=k.
在Rt△APH中,AH=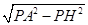 =
= ,
,
∴OA=OH—AH=k- .
.
∴A(k- ,0). …………………………3分
,0). …………………………3分
∵由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知, PH垂直平分AB.

∴OB=OA+2AH= k- +2
+2 =k+
=k+ ,
,
∴B(k+ ,0). ……………………………………………………………………4分
,0). ……………………………………………………………………4分
故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k.
可设该抛物线解析式为y=a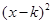 +h. …………………………………………………5分
+h. …………………………………………………5分
又抛物线过C(0,1), B(k+ ,0), 得:
,0), 得:
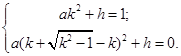
解得a=1,h=1-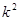 . …………………7分
. …………………7分
∴抛物线解析式为y=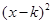 +1-
+1-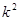 .……8分
.……8分
(2)由(1)知抛物线顶点D坐标为(k, 1-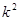 )
)
∴DH=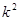 -1.
-1.
若四边形ADBP为菱形.则必有PH=DH.………………………………………………10分
∵PH=1,∴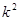 -1=1.
-1=1.
又∵k>1,∴k=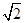 …………………………………………………………11分
…………………………………………………………11分
∴当k取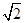 时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分
时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分
(1)连接PC,过P点作PH⊥x轴,垂足为H,根据圆的切线性质,可知PC⊥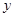 轴,由勾股定理及垂径定理,C (0,1)可得到A
轴,由勾股定理及垂径定理,C (0,1)可得到A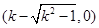 ,B
,B 即可
即可
(2)根据菱形的对角线互相平分,则有 ,得到关于
,得到关于 的方程即可
的方程即可

∵⊙P与
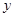 轴相切于点C (0,1),
轴相切于点C (0,1), ∴PC⊥
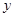 轴.
轴.∵P点在反比例函数
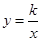 的图象上,
的图象上,∴P点坐标为(k,1). …………………2分
∴PA=PC=k.
在Rt△APH中,AH=
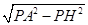 =
= ,
,∴OA=OH—AH=k-
 .
. ∴A(k-
 ,0). …………………………3分
,0). …………………………3分∵由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知, PH垂直平分AB.

∴OB=OA+2AH= k-
 +2
+2 =k+
=k+ ,
,∴B(k+
 ,0). ……………………………………………………………………4分
,0). ……………………………………………………………………4分故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k.
可设该抛物线解析式为y=a
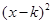 +h. …………………………………………………5分
+h. …………………………………………………5分又抛物线过C(0,1), B(k+
 ,0), 得:
,0), 得: 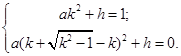
解得a=1,h=1-
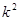 . …………………7分
. …………………7分∴抛物线解析式为y=
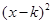 +1-
+1-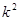 .……8分
.……8分(2)由(1)知抛物线顶点D坐标为(k, 1-
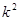 )
)∴DH=
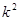 -1.
-1. 若四边形ADBP为菱形.则必有PH=DH.………………………………………………10分
∵PH=1,∴
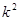 -1=1.
-1=1. 又∵k>1,∴k=
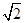 …………………………………………………………11分
…………………………………………………………11分∴当k取
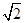 时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分
时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分(1)连接PC,过P点作PH⊥x轴,垂足为H,根据圆的切线性质,可知PC⊥
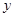 轴,由勾股定理及垂径定理,C (0,1)可得到A
轴,由勾股定理及垂径定理,C (0,1)可得到A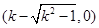 ,B
,B 即可
即可(2)根据菱形的对角线互相平分,则有
 ,得到关于
,得到关于 的方程即可
的方程即可
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
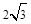 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=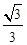 ,抛物线C经过A、P两点。
,抛物线C经过A、P两点。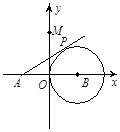
 ,
, 的点共有 个;
的点共有 个;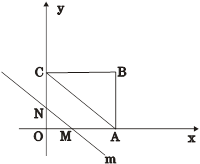
 烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度
烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度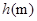 与飞行时间
与飞行时间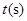 的关系式是
的关系式是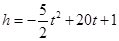 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )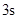
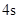
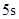
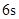
 ,我们把使函数值等于
,我们把使函数值等于 的实数
的实数 叫做这个函数的零点,则二次函数
叫做这个函数的零点,则二次函数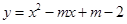 (
(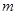 为实数)的零点的个数是( )
为实数)的零点的个数是( ) 的图象如图所示,若
的图象如图所示,若
 ,
, ,则
,则




 图像的一部分,该图在
图像的一部分,该图在 轴右侧与
轴右侧与 轴交点的坐标是
轴交点的坐标是