题目内容
【题目】如图,在数轴上点A所表示的数是![]() ,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
,点B在点A的右侧,AB=6;点C在AB之间, AC=2BC.
(1)在数轴上描出点B;
(2)求点C所表示的数,并在数轴上描出点C;
(3)已知在数轴上存在点P,使PA+PC=PB,求点P所表示的数.
![]()
【答案】(1)见解析;(2)-1,图见解析;(3)-3或-7.
【解析】
(1)根据点A和AB之间的距离即可找到点B的位置;
(2)解法一:根据AC=2BC和AB=6求出B、C之间的距离,再利用点B的位置即可得出点C所表示的数;
解法二:利用方程的思想,将BC设为x,通过AB=6建立一个关于x的方程并解方程,再利用点B的位置即可得出点C所表示的数;
解法三:设点C所表示的数为x,将AC,BC表示出来,建立方程求解即可;
(3)解法一:因为PA+PC=PB,分①当点P在AC之间时,②当点P在点A左侧时两种情况分情进行讨论即可;
解法二:利用PA =PB-PC=BC=2直接找到A,P之间的距离即可得出答案.
解:(1)点B在数轴上的位置如图1所示.
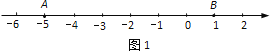
(2)解法一:因为AC=2BC,点C在AB之间,
所以AB=AC+BC=3BC.
因为AB=1-(-5)=6,
所以BC=2.
因为点B所表示的数是1,
1-2=-1
所以点C所表示的数是-1.
解法二:设BC=x,则AC=2x.
因为AB=1-(-5)=6,
所以x+2x=6.
解得x=2.
因为点B所表示的数是1,
1-2=-1
所以点C所表示的数是-1.
解法三:设点C所表示的数为x.
因为点C在AB之间,
所以BC=1-x,AC=x-(-5)= x +5.
因为AC=2BC,
所以x +5=2(1-x).
解得x=-1
点C在数轴上的位置如图2所示.
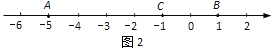
(3)解法一:因为PA+PC=PB,
所以点P在点C左侧.
因为点A表示的数是-5,点B表示的数是1,点C表示的数是-1,
所以AC =-1-(-5)=4,AB=1-(-5)=6.
①当点P在AC之间时,
设PA=x,则PC = AC- PA =4-x.
所以PB=PC+ BC =4-x +2=6-x.
因为PA+PC=PB,
所以x+4-x=6-x.
解得 x=2.
因为点A所表示的数是-5,-5+2=-3,
此时点P所表示的数是-3.
②当点P在点A左侧时,
设PA=x,则PC = PA+ AC =4+x,PB=PA+ AB =x +6,
因为PA+PC=PB,
所以x+4+x=6+x.
解得 x=2.
因为点A所表示的数是-5,-5-2=-7,
此时点P所表示的数是-7.
所以点P所表示的数是-3或-7.
解法二:因为PA+PC=PB,
所以点P在点C左侧.
所以PA =PB-PC=BC=2.
因为点A所表示的数是-5,
所以点P所表示的数是-3或-7.