��Ŀ����
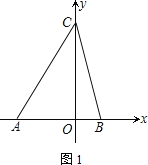
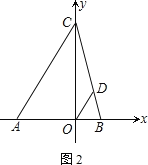
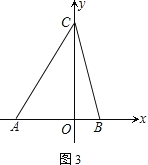
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�����������ᡱ��ͼ�е�A��ʾ��6����B��ʾ8����C��ʾ16�����dzƵ�A�͵�C�����������22�����ȵ�λ������P�ӵ�A��������1��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������2��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮
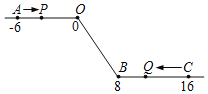
��1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
���𰸡���1����P�ӵ�A�˶���C����Ҫ��ʱ����32�룻��2��������M����Ӧ������0����3��tΪ2s����4.4sʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
��������
��1������ʱ�䣽![]() ���ֶ����ÿ�������ϵ�ʱ������ͼ��ɣ�
���ֶ����ÿ�������ϵ�ʱ������ͼ��ɣ�
��2��P��Q��������ʱ������ʱ����ȣ����ݵ�����ϵ����һԪһ�η��̣�
��3������P��O���������������ij�����Q��B���������������ij�����ȿ����ж�ʱ����ȣ����ݵ�����ϵ����һԪһ�η��̣�ͬʱ��Ҫ��������ۣ�����ȻPO��OP����PO��OP����ͬһ���߶Σ�
�⣺��1����P�ӵ�A�˶���C����Ҫ��ʱ��
t��6��1+8��0.5+��16��8����1��32���룩
�𣺵�P�ӵ�A�˶���C����Ҫ��ʱ����32��
��2�������֪��P��Q�����������߶�OB����M������OM��x����
6��1+x��0.5��8��2+��8��x����4
���x��0
��OM��0��ʾP��Q�����������߶�OB����O������������M����Ӧ������0��
��3��P��O���������������ij�����Q��B���������������ij��������2�ֿ��ܣ�
������P��AO�ϣ�����Q��CB�ϣ�
��6��t��8��2t
��ã�t��2��
������P��AO�ϣ�����Q��BO�ϣ�
��6��t��4��t��4��
��ã�t��4.4
��tΪ2s����4.4sʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�

 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�