题目内容
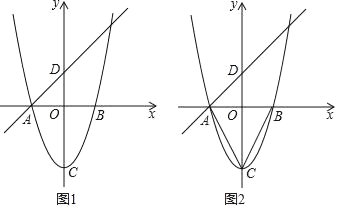
【题目】如图,已知二次函数y=x2﹣4的图象与x轴交于点A、B(点A位于点B的左侧),C为顶点.一次函数y=mx+2的图象经过点A,与y轴交于点D.
(1)求直线AD的函数表达式;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′.若新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,且当1≤x≤3时,新抛物线对应的函数值有最小值为﹣1,求新抛物线对应的函数表达式;
(3)如图,连接AC、BC,在坐标平面内,直接写出使得△ACD与△EBC相似(其中点A与点E是对应点)的点E的坐标.
【答案】(1)y=x+2;(2)y=(x+1)2﹣5或y=(x﹣3)2﹣1;(3)点E坐标为:(﹣![]() ,﹣2)或(2,﹣
,﹣2)或(2,﹣![]() )或(0,﹣
)或(0,﹣![]() )或(
)或(![]() ,﹣2).
,﹣2).
【解析】
(1)令二次函数y=x2﹣4=0,求出点A,B的坐标,把点A的坐标代入一次函数y=mx+2,即可求出直线AD的函数表达式;
(2)求出顶点C的坐标,根据CC'∥AD,求出CC'解析式,设C'(t,t﹣4),则新抛物线对应的函数表达式为:![]() ,分
,分![]() ,1≤t≤3,
,1≤t≤3,![]() 三种情况进行讨论.
三种情况进行讨论.
(3)分△ACD∽△EBC和△ACD∽△ECB两种情况进行讨论.
解:(1)当y=0时,0=x2﹣4,
∴x1=2,x2=﹣2,
∴A(﹣2,0),B(2,0)
∵直线AD过点A,
∴0=﹣2m+2,
∴m=1
∴直线AD的函数表达式为:y=x+2
(2)当x=0时,y=0﹣4=﹣4
∴C(0,﹣4)
∵CC'∥AD
∴CC'解析式为:y=x﹣4
∴设C'(t,t﹣4),则新抛物线对应的函数表达式为:y=(x﹣t)2+t﹣4
①当t<1时,1≤x≤3对应的新抛物线部分位于对称轴右侧,且y随x的增大而增大,
∴当x=1时,y最小=(1﹣t)2+t﹣4=﹣1
∴t1=2(舍去),t2=﹣1
∴y=(x+1)2﹣5
②当1≤t≤3时,
∴x=t时,y最小=t﹣4=﹣1
∴t=3
∴y=(x﹣3)2﹣1
③当t>3时,1≤x≤3对应的新抛物线部分位于对称轴左侧,且y随x的增大而减小
∴x=3时,y最小=(3﹣t)2+t﹣4=﹣1
∴t1=2(舍去),t2=3(舍去)
综上所述:新抛物线对应的函数表达式为y=(x+1)2﹣5或y=(x﹣3)2﹣1
(3)△ACD与△EBC相似
∵点A(﹣2,0),点D(0,2),点C(0,﹣4),点B(2,0)
∴![]() ,
,
设点E坐标为(x,y),
若△ACD∽△EBC
∴![]()
∴![]()
∴![]()
∴(x﹣2)2+(y﹣0)2=![]()
(x﹣0)2+(y+4)2=![]()
∴解得: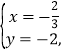
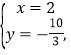
∴点E坐标![]() 或
或![]()
若△ACD∽△ECB
∴![]()
∴![]()
∴![]()
∴x2+(y+4)2=![]() (x﹣2)2+y2=
(x﹣2)2+y2=![]()
解得: 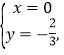

∴点E坐标![]() 或
或![]()
综上所述:点E坐标为:![]() 或
或![]() 或
或![]() 或
或![]()

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】合肥市教育教学研究室为了了解该市所有毕业班学生参加2019年安徽省中考一模考试的数学成绩情况(满分:150分,等次:![]() 等,130分
等,130分![]() 150分;
150分;![]() 等,110分
等,110分![]() 129分;C等,90分
129分;C等,90分![]() 109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
2019年合肥市一模数学成绩频数分布表
等次 | 频数 | 频率 |
| 0.2 | |
| ||
| 6 | |
| 2 | 0.1 |
合计 | 1 |
2019年合肥市一模教学成绩频数分布直方图
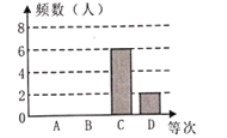
根据图表中的信息,下列说法不正确的是( )
A. 这次抽查了20名学生参加一模考试的数学成绩
B. 这次一模考试中,考试数学成绩为![]() 等次的频率为0.4
等次的频率为0.4
C. 根据频数分布直方图制作的扇形统计图中等次![]() 所占的圆心角为
所占的圆心角为![]()
D. 若全市有20000名学生参加中考一模考试,则估计数学成绩达到![]() 等次及以上的人数有12000人
等次及以上的人数有12000人