题目内容
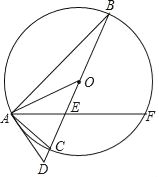
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由BC是⊙O的直径,得到∠BAF+∠FAC=90°,等量代换得到∠D+∠AOD=90°,于是得到结论;
(2)连接BF,根据相似三角形的判定和性质即可得到结论.
(1)∵BC是⊙O的直径,∴∠BAF+∠FAC=90°.
∵∠D=∠BAF,∠AOD=∠FAC,∴∠D+∠AOD=90°,∴∠OAD=90°,∴AD是⊙O的切线;
(2)连接BF.
∵∠FAC=∠AOD,∠ACE=∠ACE,∴△ACE∽△OCA,∴![]() ,∴
,∴![]() ,∴AC=AE
,∴AC=AE![]() .
.
∵∠CAE=∠CBF,∠AEC=∠BEF,∴△ACE∽△BFE,∴![]() ,∴
,∴![]() ,∴EF
,∴EF![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目