题目内容
【题目】如图,AB分别是⊙O的直径,AC是弦,DC是⊙O的切线,C为切点,AD⊥DC于点D.
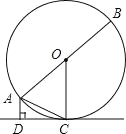
(1)已知∠ACD=a,求∠AOC的大小;
(2)求证:AC2=AB·AD.
【答案】(1)2α;(2)证明见解析.
【解析】
试题分析:(1)由CD是⊙O的切线得到∠OCD=90°,即∠ACD+∠ACO=90°,利用OC=OA得到∠ACO=∠CAO,然后利用三角形的内角和即可证明题目的结论;
(2)如图,连接BC.由AB是直径得到∠ACB=90°,然后利用已知条件可以证明在Rt△ACD∽Rt△ABC,接着利用相似三角形的性质即可解决问题.
试题解析:(1)∵CD是⊙O的切线,
∴∠OCD=90°,
即∠ACD+∠ACO=90°,①
∵OC=OA,
∴∠ACO=∠CAO,
∴∠AOC=180°-2∠ACO,即∠AOC+2∠ACO=180°,
两边除以2得:![]() ∠AOC+∠ACO=90°,②
∠AOC+∠ACO=90°,②
由①,②,得:∠ACD-![]() ∠AOC=0,
∠AOC=0,
即∠AOC=2∠ACD=2α;
(2)如图,连接BC.
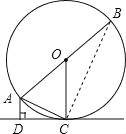
∵AB是直径,
∴∠ACB=90°,
在Rt△ACD与Rt△ABC中,
∵∠AOC=2∠B,
∴∠B=∠ACD,
∴Rt△ACD∽Rt△ABC,
∴![]() ,即AC2=AB·AD.
,即AC2=AB·AD.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
