ЬтФПФкШн
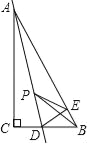
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=6cmЃЌBC=8cmЃЌЖЏЕуPДгЕуBГіЗЂЃЌдкBAБпЩЯвдУПУы5cmЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂЃЌдкCBБпЩЯвдУПУы4cmЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЃМ2ЃЉЃЌСЌНгPQЃЎ

ЃЈ1ЃЉШєЁїBPQгыЁїABCЯрЫЦЃЌЧѓtЕФжЕЃЛ
ЃЈ2ЃЉСЌНгAQЃЌCPЃЌШєAQЁЭCPЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉЪджЄУїЃКPQЕФжаЕудкЁїABCЕФвЛЬѕжаЮЛЯпЩЯЃЎ
ЁОД№АИЁПЃЈ1ЃЉt=1Лђ![]() ЪБЃЌЁїBPQгыЁїABCЯрЫЦЃЛЃЈ2ЃЉt=
ЪБЃЌЁїBPQгыЁїABCЯрЫЦЃЛЃЈ2ЃЉt=![]() ЃЛЃЈ3ЃЉжЄУїМћНтЮі.
ЃЛЃЈ3ЃЉжЄУїМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЗжСНжжЧщПіЬжТлЃКЂйЕБЁїBPQЁзЁїBACЪБЃЌ ![]() ЃЌЕБЁїBPQЁзЁїBCAЪБЃЌ
ЃЌЕБЁїBPQЁзЁїBCAЪБЃЌ ![]() ЃЌдйИљОнBP=5tЃЌQC=4tЃЌAB=10cmЃЌBC=8cmЃЌДњШыМЦЫуМДПЩЃЛ
ЃЌдйИљОнBP=5tЃЌQC=4tЃЌAB=10cmЃЌBC=8cmЃЌДњШыМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЙ§PзїPMЁЭBCгкЕуMЃЌAQЃЌCPНЛгкЕуNЃЌдђгаPB=5tЃЌPM=3tЃЌMC=8-4tЃЌИљОнЁїACQЁзЁїCMPЃЌЕУГі![]() ЃЌДњШыМЦЫуМДПЩЃЛ
ЃЌДњШыМЦЫуМДПЩЃЛ
ЃЈ3ЃЉзїPEЁЭACгкЕуEЃЌDFЁЭACгкЕуFЃЌЯШЕУГіDF=![]() ЃЌдйАбQC=4tЃЌPE=8-CM=8-4tДњШыЧѓГіDFЃЌЙ§BCЕФжаЕуRзїжБЯпЦНаагкACЃЌЕУГіRC=DFЃЌDдкЙ§RЕФжаЮЛЯпЩЯЃЌДгЖјжЄГіPQЕФжаЕудкЁїABCЕФвЛЬѕжаЮЛЯпЩЯЃЎ
ЃЌдйАбQC=4tЃЌPE=8-CM=8-4tДњШыЧѓГіDFЃЌЙ§BCЕФжаЕуRзїжБЯпЦНаагкACЃЌЕУГіRC=DFЃЌDдкЙ§RЕФжаЮЛЯпЩЯЃЌДгЖјжЄГіPQЕФжаЕудкЁїABCЕФвЛЬѕжаЮЛЯпЩЯЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпAC=6cmЃЌBC=8cmЃЌ
ЁрAB=![]() =10cmЃЌ
=10cmЃЌ
ЂйЕБЁїBPQЁзЁїBACЪБЃЌ
Ёп![]() ЃЌBP=5tЃЌQC=4tЃЌAB=10cmЃЌBC=8cmЃЌ
ЃЌBP=5tЃЌQC=4tЃЌAB=10cmЃЌBC=8cmЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрt=1ЃЛ
ЂкЕБЁїBPQЁзЁїBCAЪБЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрt=![]() ЃЌ
ЃЌ
Ёрt=1Лђ![]() ЪБЃЌЁїBPQгыЁїABCЯрЫЦЃЛ
ЪБЃЌЁїBPQгыЁїABCЯрЫЦЃЛ
ЃЈ2ЃЉШчЭМЫљЪОЃЌЙ§PзїPMЁЭBCгкЕуMЃЌAQЃЌCPНЛгкЕуNЃЌдђгаPB=5tЃЌPM=PBsinB=3tЃЌBM=4tЃЌMC=8-4tЃЌ
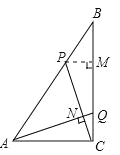
ЁпЁЯNAC+ЁЯNCA=90ЁуЃЌЁЯPCM+ЁЯNCA=90ЁуЃЌ
ЁрЁЯNAC=ЁЯPCMЧвЁЯACQ=ЁЯPMC=90ЁуЃЌ
ЁрЁїACQЁзЁїCMPЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃКt=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃЌзїPMЁЭBCгкЕуMЃЌPQЕФжаЕуЩшЮЊDЕуЃЌдйзїPEЁЭACгкЕуEЃЌDFЁЭACгкЕуFЃЌ
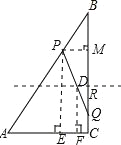
ЁпЁЯACB=90ЁуЃЌ
ЁрDFЮЊЬнаЮPECQЕФжаЮЛЯпЃЌ
ЁрDF=![]() ЃЌ
ЃЌ
ЁпQC=4tЃЌPE=8-BM=8-4tЃЌ
ЁрDF=![]() =4ЃЌ
=4ЃЌ
ЁпBC=8ЃЌЙ§BCЕФжаЕуRзїжБЯпЦНаагкACЃЌ
ЁрRC=DF=4ГЩСЂЃЌ
ЁрDдкЙ§RЕФжаЮЛЯпЩЯЃЌ
ЁрPQЕФжаЕудкЁїABCЕФвЛЬѕжаЮЛЯпЩЯЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПМзЁЂввЁЂБћШ§ЮЛбЁЪжИї10ДЮЩфЛїГЩМЈЕФЦНОљЪ§КЭЗНВюЭГМЦШчБэЃК
бЁЪж | Мз | вв | Бћ |
ЦНОљЪ§ | 9.3 | 9.3 | 9.3 |
ЗНВю | 0.026 | a | 0.032 |
вбжЊввЪЧГЩМЈзюЮШЖЈЕФбЁЪжЃЌЧвввЕФ10ДЮЩфЛїГЩМЈВЛЖМвЛбљЃЌдђaЕФжЕПЩФмЪЧЃЈЁЁЁЁЃЉ
A. 0B. 0.020C. 0.030D. 0.035