Question

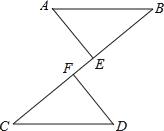
【题目】如图，AB∥CD，AB=CD，点E、F在BC上，且BE=CF．

（1）求证：△ABE≌△DCF；

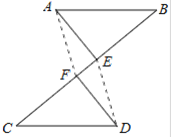
（2）连接AF，DE，试证明：四边形AFDE是平行四边形．

Answer 1

【答案】证明：（1）如图，∵AB∥CD，

∴∠B=∠C．

∵在△ABE与△DCF中，

AB＝CD， ∠B＝∠C， BE＝CF，

∴△ABE≌△DCF（SAS）；

（2）如图，连接AF、DE．

由（1）知，△ABE≌△DCF，

∴AE=DF，∠AEB=∠DFC，

∴∠AEF=∠DFE，

∴AE∥DF，

∴以A、F、D、E为顶点的四边形是平行四边形．

【解析】（1）由全等三角形的判定定理SAS证得△ABE≌△DCF；（2）利用（1）中的全等三角形的对应角相等证得∠AEB=∠DFC，则∠AEF=∠DFE，所以根据平行线的判定可以证得AE∥DF．由全等三角形的对应边相等证得AE=DF，则易证得结论．