题目内容
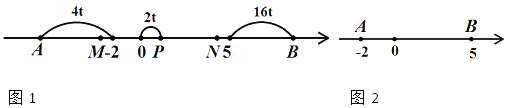
【题目】如图1，已知数轴上两点A、B对应的数分别为﹣2、5，点P为数轴上的一动点，其对应的数为x．
（1）PA= ；PB= （用含x的式子表示）
（2）在数轴上是否存在点P，使PA+PB=10？若存在，请直接写出x的值；若不存在，请说明理由．
（3）如图2，点P以2个单位/s的速度从点O向右运动，同时点A以4个单位/s的速度向左运动，点B以16个单位/s的速度向右运动，在运动过程中，M、N分别是AP、OB的中点，问： 
的值是否发生变化？请说明理由．
【答案】（1）|x+2|，|x﹣5|；（2）x=6.5或﹣3.5；（3）不发生变化，理由见解析.
【解析】试题分析：（1）根据数轴上两点之间的距离求法得出PA，PB的长；
（2）分三种情况：①当点P在A、B之间时，②当点P在B点右边时，③当点P在A点左边时，分别求出即可；
（3）根据题意用t表示出AB，OP，MN的长，进而求出答案．
试题解析：（1）∵数轴上两点A.B对应的数分别为2、5，点P为数轴上的一动点，其对应的数为x，
∴PA=|x+2|;PB=|x5|(用含x的式子表示).
故答案为：|x+2|，|x5|；
（2）分三种情况：
①当点P在A、B之间时，PA+PB=10，故舍去．
②当点P在B点右边时，PA=x+2，PB=x﹣5，
∴（x+2）+（x﹣5）=10，
∴x=6.5；
③当点P在A点左边时，PA=﹣x﹣2，PB=5﹣x，
∴（﹣x﹣2）+（5﹣x）=10，
∴x=﹣3.5；
（3）
的值不发生变化．
理由：设运动时间为t分钟．
则P表示2t，A表示-2-4t，B表示5+16t，M表示-1-t，N表示2.5+8t，
AB=20t+7OP=2t，
MN=2.5+8t-（-1-t）=9t+3.5，
∴
，
∴在运动过程中，M、N分别是AP、OB的中点， 
的值不发生变化．
