Question

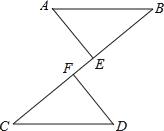
【题目】如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．

（1）当∠E=∠F时，则∠ADC=_____°；

（2）当∠A=55°，∠E=30°时，求∠F的度数；

（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．

Answer 1

【答案】（1）90°；（2）∠F=40°；（3）∠A=．

【解析】（1）∵∠E=∠F，∠DCE=∠BCF，∠ADC=∠E+∠DCE，∠ABC=∠BCF+∠F，

∴∠ADC=∠ABC，

∵四边形ABCD是⊙O的内接四边形，

∴∠ADC+∠ABC=180°，

∴∠ADC=90°．

故答案为：90°；

（2）∵在△ABE中，∠A=55°，∠E=30°，

∴∠ABE=180°﹣∠A﹣∠E=95°，

∴∠ADF=180°﹣∠ABE=85°，

∴在△ADF中，∠F=180°﹣∠ADF﹣∠A=40°；

（3）∵∠ADC=180°﹣∠A﹣∠F，∠ABC=180°﹣∠A﹣∠E，

∵∠ADC+∠ABC=180°，

∴180°﹣∠A﹣∠F+180°﹣∠A﹣∠E=180°，

∴2∠A+∠E+∠F=180°，

∴∠A==．