题目内容
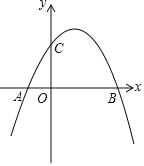
【题目】如图,抛物线 y=﹣![]() x2+
x2+![]() x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
(1)求 A,B,C的坐标;
(2)直线 l:y=﹣![]() x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
【答案】(1)A(﹣1,0);B(4,0);C(0,2);(2)图形见解析;四边形ACBD为矩形.
【解析】
(1)分别代入x=0,y=0求出与之对应的y,x的值,进而即可得出点A,B,C的坐标;
(2)利用一次函数图象上点的坐标特征可求出点D的坐标,依照题意画出图形,设CD交AB于点E,利用一次函数图象上点的坐标特征可求出点E的坐标,结合点A,B,C的坐标可得出AB=CD,AB,CD互相平分,利用矩形的判定定理即可证出四边形ACBD为矩形.
(1)当x=0时,y![]() x2
x2![]() x+2=2,∴点C的坐标为(0,2).
x+2=2,∴点C的坐标为(0,2).
当y=0时,有![]() x2
x2![]() x+2=0,解得:x1=﹣1,x2=4,∴点A的坐标为(﹣1,0),点B的坐标为(4,0).
x+2=0,解得:x1=﹣1,x2=4,∴点A的坐标为(﹣1,0),点B的坐标为(4,0).
(2)∵点D(m,﹣2)在直线y![]() x+2上的,∴﹣2
x+2上的,∴﹣2![]() m+2,解得:m=3,∴点D的坐标为(3,﹣2).
m+2,解得:m=3,∴点D的坐标为(3,﹣2).
依照题意画出图形,设CD交AB于点E,如图所示,四边形ACBD为矩形.理由如下:
当y=0时,有![]() x+2=0,解得:x
x+2=0,解得:x![]() ,∴点E的坐标为(
,∴点E的坐标为(![]() ,0).
,0).
∵A(﹣1,0),B(4,0),C(0,2),D(3,﹣2),E(![]() ,0),∴AB=4﹣(﹣1)=5,CD
,0),∴AB=4﹣(﹣1)=5,CD![]() 5,CE
5,CE![]() ,AE
,AE![]() (﹣1)
(﹣1)![]() ,∴AE
,∴AE![]() AB,CE
AB,CE![]() CD,∴AB=CD,AB,CD互相平分,∴四边形ACBD为矩形.
CD,∴AB=CD,AB,CD互相平分,∴四边形ACBD为矩形.

练习册系列答案
相关题目