题目内容
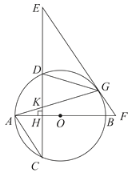
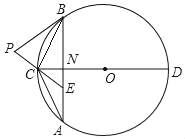
【题目】如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,BC,点E在AB上,且AE=CE.
(1)求证:∠ABC=∠ACE;
(2)过点B作⊙O的切线交EC的延长线于点P,证明PB=PE;
(3)在第(2)问的基础上,设⊙O半径为2![]() ,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.
,若点N为OC中点,点Q在⊙O上,求线段PQ的最大值.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)因为直径CD垂直于不过圆心O的弦AB,垂足为点N,所以![]() ,所以∠CAE=∠ABC,因为AE=CE,所以∠CAE=∠ACE,所以∠ABC=∠ACE;
,所以∠CAE=∠ABC,因为AE=CE,所以∠CAE=∠ACE,所以∠ABC=∠ACE;
(2)连接OB,设∠CAE=∠ACE=∠ABC=x,通过计算可得∠PEB=∠PBE=2x,所以PB=PE;
(3)连接OP,证明△OBC和△PBE为等边三角形,因为⊙O半径为2![]() ,可得BN=3,NE=1,即PB=BE=4,在Rt△PBO中求得PO的长,即可得出PQ的最大值.
,可得BN=3,NE=1,即PB=BE=4,在Rt△PBO中求得PO的长,即可得出PQ的最大值.
解:(1)证明:∵直径CD垂直于不过圆心O的弦AB,垂足为点N,
∴![]() ,
,
∴∠CAE=∠ABC,
∵AE=CE,
∴∠CAE=∠ACE,
∴∠ABC=∠ACE;
(2)如图,连接OB,
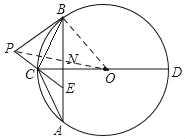
∵过点B作⊙O的切线交EC的延长线于点P,
∴∠OBP=90°,
设∠CAE=∠ACE=∠ABC=x,
则∠PEB=2x,
∵OB=OC,AB⊥CD,
∴∠OBC=∠OCB=90°﹣x,
∴∠BOC=180°﹣2(90°﹣x)=2x,
∴∠OBE=90°﹣2x,
∴∠PBE=90°﹣(90°﹣2x)=2x,
∴∠PEB=∠PBE,
∴PB=PE;
(3)如图,连接OP,
∵点N为OC中点,AB⊥CD,
∴AB是CD的垂直平分线,
∴BC=OB=OC,
∴△OBC为等边三角形,
∵⊙O半径为![]() ,
,
∴CN=![]() ,
,
∵∠CAE=∠ACE=![]() ∠BOC=30°,
∠BOC=30°,
∴∠CEN=60°,∠PBE=2∠CAB=60°,
∴△PBE为等边三角形,BN=3,NE=1,
∴PB=BE=BN+NE=3+1=4,
∴PO=![]() =
=![]() ,
,
∴PQ的最大值为PO+![]() =
=![]() +
+![]() .
.

 名校课堂系列答案
名校课堂系列答案