题目内容
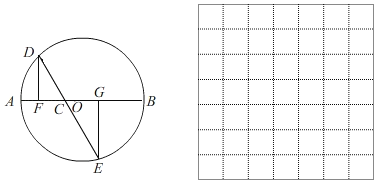
【题目】如图,在△ABC中,AB=AC=4,以AB为直径的⊙O交BC于点D,交AC于点E,点P是AB的延长线上一点,且∠PDB=![]() ∠A,连接DE,OE.
∠A,连接DE,OE.
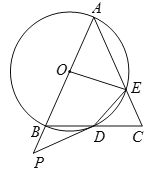
(1)求证:PD是⊙O的切线.
(2)填空:①当∠P的度数为______时,四边形OBDE是菱形;
②当∠BAC=45°时,△CDE的面积为_________.
【答案】(1)见解析;(2)①30;②![]()
【解析】
(1)连接OD,由三角形内角和定理可证∠ODB=90°-![]() ∠A,进而可求∠ODB+∠PDB=90°,即∠ODP为直角,从而结论得证;
∠A,进而可求∠ODB+∠PDB=90°,即∠ODP为直角,从而结论得证;
(2)当四边形OBDE为菱形时,△OBD为等边三角形,则∠P为30°;
(3)连接BE,AD,由圆周角定理可证∠ADB=90°,∠AEB=90°,由等腰三角形的性质和三角形的面积公式可知S△DCE=![]() S△BCE,证明△ABE是等腰直角三角形,根据勾股定理求出AE=BE=
S△BCE,证明△ABE是等腰直角三角形,根据勾股定理求出AE=BE=![]() ,然后根据三角形面积公式求解即可.
,然后根据三角形面积公式求解即可.
解:(1)连接OD,
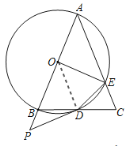
∵OB=OD, ∠PDB=![]() ∠A,
∠A,
∴∠ODB=∠ABD=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A=90°-∠PDB,
∠A=90°-∠PDB,
∴∠ODB+∠PDB=90°,
∴∠ODP=90°,
∵OD是⊙O的半径,
∴PD是⊙O的切线.
(2)①30°,理由如下:
若四边形OBDE为菱形,则OB=BD=DE=EO=OD,
∴△OBD为等边三角形,
∴∠ABD=∠ODB=60°,
∵∠PDO=90°,
∴∠PDB=30°,
∴∠P=30°,
即当∠P为30°时,四边形OBDE为菱形;
②连接BE,AD,如图,
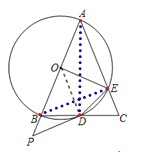
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,∠AEB=90°,
∵AB=AC,
∴D为BC中点,
∴S△DCE=![]() S△BCE,
S△BCE,
∵∠BAC=45°,
∴AE=BE,△ABE是等腰直角三角形,
∵AB=AC=4,
∴AE=BE=![]() ,
,
∴CE=4-![]() ,
,
∴S△DCE=![]() S△BCE,
S△BCE,
=![]() ×
×![]() BE·CE
BE·CE
=![]() ×
×![]() ×
×![]() ×(4-
×(4-![]() )
)
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】如图,AB是⊙O的直径,AB=4cm,C为AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=60°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=xcm,DE=ycm(当x的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为 cm(结果保留一位小数).