题目内容
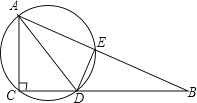
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD外接圆的直径.
【答案】(1)证明见解析;(2)3![]()
【解析】试题分析:(1)由Rt△ABC中,∠ACB=90°,可得AD是直径,可得△ADE为直角三角形,在两个直角三角形中,利用AAS可得两三角形全等,得到答案;
(2)先根据勾股定理求出AB的长,由(1)知,AC=AE,CD=DE,设CD=x,则BD=8-x,在Rt△BDE中,根据勾股定理求出x的值,同理,在Rt∠ACD中求出AD的长,进而可得出结论.
试题解析:
(1)证明:∵Rt△ABC中,∠ACB=90°,
∴AD为圆的直径,
∴∠AED=90°,
∵AD是△BAC的∠CAB的角平分线,
∴∠CAD=∠EAD,
Rt△ACD与Rt△ADE中,
∠CAD=∠BAD, ∠ACB=∠AED ,AD=AD ,
∴Rt△ACD≌Rt△ADE(AAS),
∴AC=AE.
(2)∵在Rt△ABC中,∠ACB=90°,AC=6,CB=8,
∴![]()
∵由(1)知,AC=AE,CD=DE,∠ACD=∠AED=90°,
∴设CD=x,则BD=8-x,BE=AB-AE=10-6=4,
在Rt△BDE中, ![]()
![]() ,即
,即![]()
![]() 解得x=3.
解得x=3.
在Rt△ACD中![]()
![]() 即
即![]() 解得AD=
解得AD=![]() .
.

练习册系列答案
相关题目