题目内容
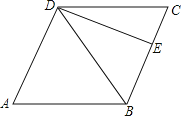
【题目】如图,菱形ABCD的边长为2,且∠ABC=120°,E是BC的中点,P为BD上一点,且△PCE的周长最小,则△PCE的周长的最小值为( )
A.![]() +1B.
+1B.![]() +1C.2
+1C.2![]() +1D.2
+1D.2![]() +1
+1
【答案】B
【解析】
由菱形ABCD中,∠ABC=120°,易得△BCD是等边三角形,继而求得∠ADE的度数;连接AE,交BD于点P;首先由勾股定理求得AE的长,即可得△PCE周长的最小值=AE+EC.
解:∵菱形ABCD中,∠ABC=120°,
∴BC=CD=AD=2,∠C=180°﹣∠ABC=60°,∠ADC=∠ABC=120°,
∴∠ADB=∠BDC=![]() ∠ADC=60°,
∠ADC=60°,
∴△BCD是等边三角形,
∵点E是BC的中点,
∴∠BDE=![]() ∠BDC=30°,
∠BDC=30°,
∴∠ADE=∠ADB+∠BDE=90°,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴PA=PC,
∵△PCE的周长=![]() ,
,
若△PCE的周长最小,即PC+PE最小,也就是PA+PE最小,即A,P,E三点共线时,
∵DE=CDsin60°=![]() ,CE=
,CE=![]() BC=1,
BC=1,
∴在Rt△ADE中,![]() ,
,
∴△PCE周长为:PC+PE+CE=PA+PE+CE=AE+CE=![]() ,
,
故选:B.

【题目】某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-3 | +7 | -9 | +8 | +6 | -5 | -4 |
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?
【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?


