题目内容
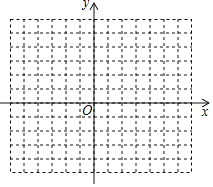
【题目】如图,△ABC在平面直角坐标系中,点A(2,﹣1),B(3,2),C(1,0).解答问题:请按要求对△ABC作如下变换.
(1)将△ABC绕点O逆时针旋转90°得到△A1B1C1;
(2)以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△A2B2C2.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据网格结构找出点A、B、C绕点O逆时针旋转90°的对应点A1、B1、C1的位置,然后顺次连接即可;
(2)连接AO并延长至A2,使A2O=2AO,连接BO并延长至B2,使B2O=2BO,连接CO并延长至C2,使C2O=2CO,然后顺次连接A2、B2、C2即可.
(1)如图所示,△A1B1C1即为△ABC绕点O逆时针旋转90°得到的图形;
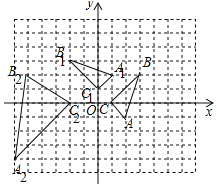
(2)如图所示,△A2B2C2即为△ABC在位似中心O的异侧位似比为2:1的图形.

练习册系列答案
相关题目
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?