题目内容
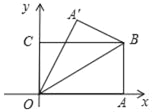
【题目】在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
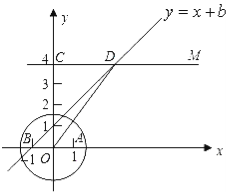
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.
【答案】(1)b=1,D(3,1);(2)(5,0)、(6,0)或(![]() ,0).
,0).
【解析】
试题(1)由点B与点A关于原点对称,且点A的坐标为(1,0),求出点B的坐标为(-1,0),把B点坐标代入y=x+b,求出b,把y=4代入即可求出点D的坐标;
(2)点P在x轴的正半轴上,△POD是等腰三角形有三种情形:1、PO=OD=5 则P(5,0);2、PD=OD=5 则PO=2×3=6 则点P(6,0); 3、PD=PO设P(x,0) D(3,4)则由勾股定理 解得x=![]() ,则点P(
,则点P(![]() ,0),
,0),
(3)由P,D两点坐标根据两圆外切满足的条件即可以算出.
试题解析:(1)点B(—1,0),代入得到b=1直线BD:y=x+1
y=4代入得x=3
∴点D(3,1)
(2)1、PO=OD=5 则P(5,0)
2、PD=OD=5 则PO=2×3=6 则点P(6,0)
3、PD=PO
设P(x,0) D(3,4)则由勾股定理解得x=![]()
则点P(![]() ,0)
,0)
(3)由P,D两点坐标可以算出:
1、当PD=2![]() 时,r=5—2
时,r=5—2![]() 2、当PD=5时,r=1 .
2、当PD=5时,r=1 .
考点: 1.一次函数;2.等腰三角形的性质;3.圆与圆的位置关系.

练习册系列答案
相关题目