题目内容
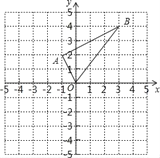
【题目】如图在平面直角坐标系中,已知点A(﹣1,2),B(3,4).
(1)画出△ABO向上平移2个单位,再向左平移4个单位后所得的图形△A′B′O′;
(2)写出A、B、O后的对应点A′、B′、O′的坐标;
(3)求两次平移过程中OB共扫过的面积.
【答案】(1)见解析;(2) A′(﹣5,4)、B′(﹣1,6)、O′(﹣4,2);(3)22.
【解析】
(1)根据网格结构找出平移后A、B、O的对应点A′、B′、O′的位置,然后顺次连接即可;
(2)根据网格结构写出点A′、B′、O′的坐标即可;
(3)分向上平移和向左平移两个部分,利用平行四边形的面积公式列式计算即可得解.
解:(1)△A′B′O′如图所示;
(2)A′(﹣5,4)、B′(﹣1,6)、O′(﹣4,2);
(3)OB向上平移2个单位扫过的面积为2×3=6,
接着向左平移4个单位扫过的面积为4×4=16,
所以平移过程中OB扫过的面积一共为6+16=22.

练习册系列答案
相关题目