题目内容
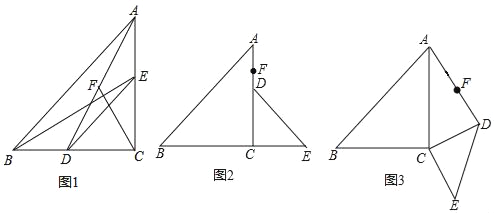
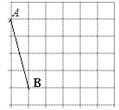
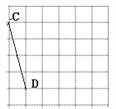
【题目】如图，P、Q是方格纸中的两格点，请按要求画出以PQ为对角线的格点四边形.（顶点都在格点上的四边形称为格点四边形）
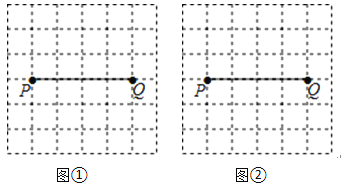
（1）在图①中画出一个面积最小的中心对称图形PAQB，
（2）在图②中画出一个四边形PCQD，使其是轴对称图形但不是中心对称图形，且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
【答案】（1）画图见解析；（2）画图见解析.
【解析】
（1）利用方格纸的特点及几何图形的计算方法，利用割补法，把四边形PAQB的面积转化为△PAQ与△PBQ的面积之和，根据两个三角形的底PQ一定时，要使面积最小，则满足高最小，且同时满足顶点都在格点上即可得答案；（2）根据题意，画出的四边形是轴对称图形但不是中心对称图形，且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到可知此四边形是等腰梯形，根据方格纸的特点，作出满足条件的图形即可.
（1）∵PQ为对角线，
∴S四边形PAQB=S△PAQ+S△PBQ，
∵PQ一定时，高最小时，△PAQ与△PBQ的面积最小，A、B在格点上，
∴高为1，
∴四边形PAQB如图①所示：
（2）∵四边形PCQD是轴对称图形但不是中心对称图形，且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到，
∴四边形PCQD是等腰梯形，
∴四边形PCQD如图②所示：
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
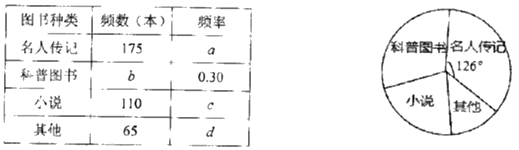
一卷搞定系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值 （单位：克） |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）这批样品的平均质量比标准质量多还是少？多或少几克？
（2）若标准质量为450克，则抽样检测的20袋食品的总质量为多少克？
（3）若该种食品的合格标准为450±5克，求该食品的抽样检测的合格率．
【题目】某新店开业宣传，进店有礼活动，店员们需准备制作圆柱体礼品纸盒（如图①），每个纸盒由1个长方形侧面和2个圆形底面组成，现有100张正方形纸板全部以A或者B方法截剪制作（如图②），设截剪时x张用A方法．
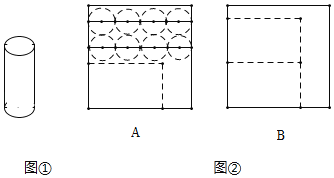
（1）根据题意，完成以下表格：
裁剪法A | 裁剪法B | |
长方形侧面 | x |
|
圆形底面 |
| 0 |
（2）若裁剪出的长方形侧面和圆形底面恰好用完，问能做多少个纸盒？
（3）按以上制作方法，若店员们希望准备300个礼盒，那至少还需要正方形纸板 张．
