Question

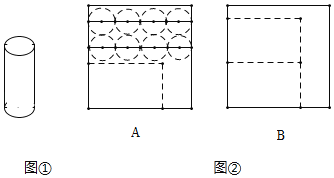
【题目】某新店开业宣传，进店有礼活动，店员们需准备制作圆柱体礼品纸盒（如图①），每个纸盒由1个长方形侧面和2个圆形底面组成，现有100张正方形纸板全部以A或者B方法截剪制作（如图②），设截剪时x张用A方法．

（1）根据题意，完成以下表格：

	裁剪法A	裁剪法B
长方形侧面	x
圆形底面		0

（2）若裁剪出的长方形侧面和圆形底面恰好用完，问能做多少个纸盒？

（3）按以上制作方法，若店员们希望准备300个礼盒，那至少还需要正方形纸板　 　张．

Answer 1

【答案】（1）2（100﹣x），8x；（2）160个；（3）88

【解析】

（1）由题意得出截剪时（100﹣x）张用B方法，一共能截剪出2（100﹣x）个长方形侧面，没有圆形底面，由每张正方形纸板用A方法截剪出8个圆形和1个长方形，得出一共能截剪出8x个圆形和x个长方形，即可得出结果；

（2）由题意得x+2（100﹣x）＝×8x，解得x＝40，则×8×40＝160；

（3）由题意得需要300×2÷8＝75（张）纸板截剪圆形底面，需要（300﹣75）÷2＝112.5≈113（张）纸板截剪长方形侧面，共用正方形纸板75+113＝188（张），则至少还需要正方形纸板188﹣100＝88（张）．

解：（1）∵设截剪时x张用A方法，

∴截剪时（100﹣x）张用B方法，

∵每张正方形纸板用B方法，只能截剪2个长方形，

∴一共能截剪出2（100﹣x）个长方形侧面，没有圆形底面，

∵每张正方形纸板用A方法截剪出8个圆形和1个长方形，

∴一共能截剪出8x个圆形和x个长方形，

故答案为：2（100﹣x），8x；

（2）若裁剪出的长方形侧面和圆形底面恰好用完，

由题意得：x+2（100﹣x）＝×8x，

解得：x＝40，

∴×8×40＝160（个）；

答：若裁剪出的长方形侧面和圆形底面恰好用完，能做160个纸盒；

（3）由题意得：需要300×2÷8＝75（张）纸板截剪圆形底面，需要（300﹣75）÷2＝112.5≈113（张）纸板截剪长方形侧面，

∴共用正方形纸板：75+113＝188（张），

∴至少还需要正方形纸板：188﹣100＝88（张），

故答案为：88．