题目内容
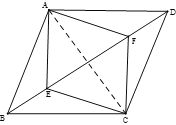
【题目】如图,在平行四边形ABCD中,点E、F在对角线BD上,且BF=DE

(1)求证:△ADE≌△CBF.
(2)若AE=3,AD=4,∠DAE=90°,该判断当BE的长度为多少时,四边形AECF为菱形,并说明理由.
【答案】(1)证明见解析;(2)BE的长度为![]() 时,四边形AECF为菱形.
时,四边形AECF为菱形.
【解析】
(1)由平行四边形的性质可得∠ADE=∠CBF,AD=BC,利用SAS即可证明△ADE≌△CBF;(2)连接AC,设BE=x,AC、EF相交于O,利用勾股定理可求出DE的长,即可用x表示出OE和OB的长,由菱形的性质可得AC⊥EF,即可证明平行四边形ABCD是菱形,可得AB=AD=4,在Rt△AOB和Rt△AOE中,分别利用勾股定理表示出OA2,列方程求出x的值即可得答案.
(1)∵平行四边形ABCD,
∴AD//BC,
∴∠∠ADE=∠CBF,AD=BC,
又∵BF=DE,
∴△ADE≌△CBF.
(2)BE的长度为![]() 时,四边形AECF为菱形.理由如下:
时,四边形AECF为菱形.理由如下:
连接AC,设BE=x,AC、EF相交于O,
∵AE=3,AD=4,∠DAE=90°,
∴BF=DE=![]() =5,
=5,
∴OE=![]() ,OB=
,OB=![]() ,
,
∵四边形AECF为菱形,
∴AC⊥EF,
∴平行四边形ABCD是菱形,
∴AB=AD=4,
在Rt△AOB和Rt△AOE中,OA2=AB2-OB2=AE2-OE2,即42-(![]() )2=32-(
)2=32-(![]() )2,
)2,
解得:x=![]() .
.
∴BE的长度为![]() 时,四边形AECF为菱形.
时,四边形AECF为菱形.

 阅读快车系列答案
阅读快车系列答案【题目】某校八年级(1)班全体学生进行了第一次体育中考模拟测试,成绩统计如下表:
成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人数(人) | 6 | 5 | 5 | 8 | 7 | 7 | 4 |
根据上表中的信息判断,下列结论中错误的是( )
A. 该班一共有42名同学
B. 该班学生这次考试成绩的众数是8
C. 该班学生这次考试成绩的平均数是27
D. 该班学生这次考试成绩的中位数是27分