Question

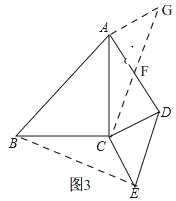
【题目】如图△ABC和△DEC都是等腰三角形，点C为它们的公共直角顶点，连AD、BE，F为线段AD的中点，连CF．

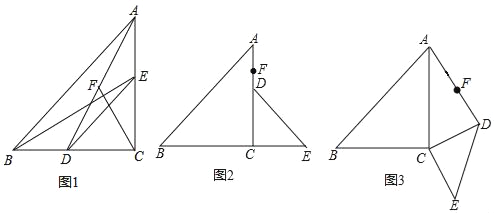
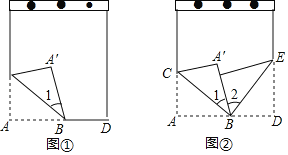
（1）如图1，当D点在BC上时，BE与CF的数量关系是　 　．

（2）如图2，把△DEC绕C点顺时针旋转90°，其他条件不变，问（1）中的关系是否仍然成立？请说明理由．

（3）如图3，把△DEC绕C点顺时针旋转一个钝角，其他条件不变，问（1）中的关系是否仍然成立？如成立请证明，如果不成立，请写出相应的正确的结论并加以证明．

Answer 1

【答案】（1）BE=2CF；（2）（1）中的关系是仍然成立，理由见解析；（3）（1）中的关系是仍然成立，理由见解析.

【解析】试题分析：（1）根据“SAS”证明△ACD≌△BCE，可得AD=BE，又因为AD=2CF，从而BE=2CF；

（2）由点F是AD中点，可得AD=2DF，从而AC= 2DF+CD，又由△ABC和△CDE是等腰直角三角形，可知BC=2DF+CE，所以BE= 2（DF+CE），CF= DF+CD，从而BE=2CF；

（3）延长CF至G使FG=CF，即：CG=2CF，可证△CDF≌△GAF，再证明△BCE≌△ACG，从而BE=CG=2CF成立.

解：（1）∵△ABC是等腰直角三角形，

∴AC=BC，

∵△CDE是等腰直角三角形，

∴CD=CE，

在△ACD和△BCE中，，

∴△ACD≌△BCE，

∴AD=BE，在Rt△ACD中，点F是AD中点，

∴AD=2CF，

∴BE=2CF，

故答案为BE=2CF；

（2）（1）中的关系是仍然成立，

理由：∵点F是AD中点，

∴AD=2DF，

∴AC=AD+CD=2DF+CD，

∵△ABC和△CDE是等腰直角三角形，

∴AC=BC，CD=CE，

∴BC=2DF+CE，

∴BE=BC+CE=2DF+CE+CE=2（DF+CE），

∵CF=DF+CD=DF+CD，

∴BE=2CF；

（3）（1）中的关系是仍然成立，理由：如图3，

延长CF至G使FG=CF，即：CG=2CF，

∵点F是AD中点，

∴AF=DF，

在△CDF和△GAF中，，

∴△CDF≌△GAF，

∴AG=CD=CE，∠CDF=∠GAF，

∴∠CAG=∠CAD+∠GAF=∠CAD+∠ADC=180°﹣∠ACD，

∵∠ACB=∠DCE=90°，

∴∠BCE=360°﹣∠ACB﹣∠DCE﹣∠ACD=180°﹣∠ACD，

∴∠CAG=∠BCE，

连接BE，

在△BCE和△ACG中，，

∴△BCE≌△ACG，

∴BE=CG=2CF，

即：BE=2CF．