Question

如图，一条直线与反比例函数y=

k

x

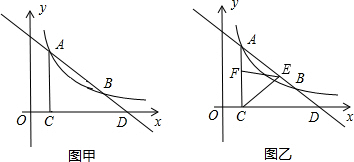
的图象交于A（1，4）、B（4，n）两点，与x轴交于D点，AC⊥x轴，垂足为C．
（1）如图甲，①求反比例函数的解析式；②求n的值及D点坐标；
（2）如图乙，若点E在线段AD上运动，连接CE，作∠CEF=45°，EF交AC于F点．
①试说明△CDE∽△EAF；
②当△ECF为等腰三角形时，直接写出F点坐标．

Answer 1

（1）①∵点A（1，4）在反比例函数图象上
∴k=4
即反比例函数关系式为y=

4

x

；
②∵点B（4，n）在反比例函数图象上
∴n=1
设一次函数的解析式为y=mx+b
∵点A（1，4）和B（4，1）在一次函数y=mx+b的图象上
∴

m+b=4 4m+b=1

解得

m=-1 b=5

∴一次函数关系式为y=-x+5
令y=0，得x=5
∴D点坐标为D（5，0）；

（2）①证明：∵A（1，4），D（5，0），AC⊥x轴
∴C（1，0）
∴AC=CD=4，
即∠ADC=∠CAD=45°，
∵∠AEC=∠ECD+∠ADC=∠ECD+45°，
∠AEC=∠AEF+∠FEC=∠AEF+45°，
∴∠ECD=∠AEF，
△CDE和△EAF的两角对应相等，
∴△CDE∽△EAF．

②当CE=FE时，由△CDE≌△EAF可得AE=CD=4，DE=AF=4﹙

2

-1），
∵A（1，4），
∴F点的纵坐标=4-AF=4-4（

2

-1）=8-4

2

∴F﹙1，8-4

2

﹚
当CE=CF时，由∠FEC=45°知∠ACE=90°，此时E与D重合，
∴F与A重合，
∴F（1，4）
当CF=EF时，由∠FEC=45°知∠CFE=90°，显然F为AC中点，
∴F（1，2）
当△ECF为等腰三角形时，点F的坐标为F1(1，2)；F2(1，4)；F3(1，8-4

2

)