题目内容
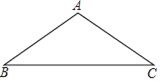
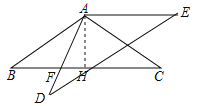
【题目】如图，在△ABC中，AB＝AC＝5，sinC＝
，将△ABC绕点A逆时针旋转得到△ADE，点B、C分别与点D、E对应，AD与边BC交于点F．如果AE∥BC，那么BF的长是____．
【答案】
【解析】
如图，过A作AH⊥BC于H，得到∠AHB=∠AHC=90°，BH=CH，根据三角函数的定义得到AH=3，求得CH=BH
4，根据旋转的性质得到∠BAF=∠CAE，根据平行线的性质得到∠CAE=∠C，从而得到∠BAF=∠B，由等角对等边得到AF=BF，设AF=BF=x，得到FH=4﹣x，根据勾股定理即可得到结论．
如图，过A作AH⊥BC于H，∴∠AHB=∠AHC=90°，BH=CH．
∵AB=AC=5，sinC
，∴AH=3，∴CH=BH4．
∵将△ABC绕点A逆时针旋转得到△ADE，∴∠BAF=∠CAE．
∵AE∥BC，∴∠CAE=∠C．
∵∠B=∠C，∴∠BAF=∠B，∴AF=BF，设AF=BF=x，∴FH=4﹣x．
∵AF2=AH2+FH2，∴x2=32+（4﹣x）2，解得：x
，∴BF．
故答案为：．
练习册系列答案
相关题目
