题目内容
【题目】在
和
中，
，
，
．
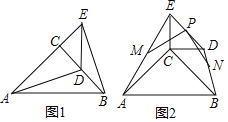
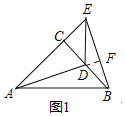
如图1，点D在BC上，求证：
，
．
将图1中的绕点C按逆时针方向旋转到图2所示的位置，旋转角为
为锐角
，线段DE，AE，BD的中点分别为P，M，N，连接PM，PN．
请直接写出线段PM，PN之间的关系，不需证明；
若
，求
．
【答案】（1）见解析；（2）
；②
.
【解析】
证明
≌
，可得
，
根据直角三角形两锐角互余可得：
，所以
；
先证明≌，得，
，再证明，根据三角形的中位线定理得：
，
，
，
，所以
，
；
证明
≌
得
根据周角定义和直角可得
的值．
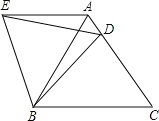
证明：如图1，延长AD交BE于F．
在和
中，
，
≌．
，
．
，
，
，
．
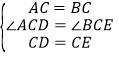解：，．
理由是：如图2，连接BE，AD，交于点Q，
，
，
即
，
在和中，
，
≌，
，，
，
，
，
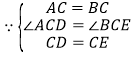是AE的中点，P是ED的中点，
，，
同理得：，，
，．
由
知，
又
，
．
在和中
，
≌
．
，
，
．
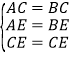练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
