Question

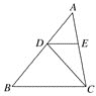
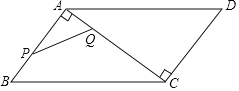
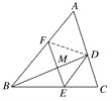
【题目】如图，BD是△ABC的角平分线，点E、F分别在BC、AB上，且DE∥AB，∠DEF＝∠A，EF与BD相交于点M，以下结论：①△BDE是等腰三角形；②四边形AFED是菱形；③BE＝AF；④若AF∶BF＝3∶4，则△DEM的面积：△BAD的面积＝9∶49，以上结论正确的是(　　)

A. ①②③④

B. ①③④

C. ①③

D. ③④

Answer 1

【答案】B

【解析】

根据BD是△ABC的角平分线与DE∥AB易证∠DBE＝∠BDE，故△BDE是等腰三角形；可证EF∥AD，四边形ADEF为平行四边形而不是菱形，即可得BE＝AF，再连接DF，得△DEM∽△BFM，再求出相似比，利用面积比等于相似比的平方即求得△DEM的面积与△BAD的面积之比.

∵BD是△ABC的角平分线，

∴∠DBE＝∠ABD，

∵DE∥AB，

∴∠ABD＝∠BDE，

∴∠DBE＝∠BDE，

∴BE＝DE，

∴△BDE是等腰三角形，故①正确；

∵DE∥AB，

∴∠BAC＋∠ADE＝180°，

∵∠DEF＝∠BAC，

∴∠DEF＋∠ADE＝180°，

∴EF∥AD，

∴四边形ADEF为平行四边形，故②错误；

∴AF＝DE，

∴BE＝AF；故③正确；

如图，连接DF，

∵DE∥AB，

∴△DEM∽△BFM，

∴＝，

∵DE＝AF，AF∶BF＝3∶4，

∴＝＝，＝＝，

∴＝，

∴S四边形AFMD＝S△DEM，S△BFM＝S△DEM，

∴△DEM的面积∶△BAD的面积＝9∶49，故④正确，

故选B.