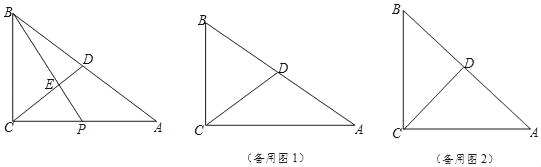
��Ŀ����
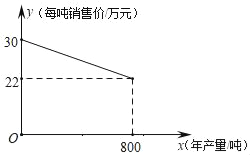
����Ŀ����֪����������Ʒ������ij�ֲ�Ʒ�������������800�֣������ò�Ʒÿ��������ط�Ϊ10��Ԫ�����������IJ�Ʒ�����ڵ��������꣮��Ʒÿ���ۼ�y����Ԫ���������x���֣�֮��ĺ�����ϵ��ͼ��ʾ
��1�����ò�Ʒ�����Ϊ���ٶ�ʱ������ɻ��7500��Ԫë����ë�������۶��ط��ã�
��2�����ò�Ʒ�����Ϊ���ٶ�ʱ���ó��ܻ�õ������۵��Ǵ�ë�������ë���������Ԫ��
���𰸡���1�����ò�Ʒ�����Ϊ500��ʱ������ɻ��7500��Ԫë����2�����ò�Ʒ�����Ϊ800��ʱ���ó��ܻ�õ������۵����ë�������ë������9600��Ԫ��
��������
��1���������������ò�Ʒÿ���ۼ�y����Ԫ���������x���֣�֮��ĺ�����ϵʽ���Ӷ������г���Ӧ�ķ��̣�������Խ����
��2����������ͣ�1���еĺ�����ϵʽ��������õ��ò�Ʒ�����Ϊ���ٶ�ʱ���ó��ܻ�õ������۵����ë�������ë���������Ԫ��
��1�����Ʒÿ���ۼ�y����Ԫ���������x���֣�֮��ĺ�����ϵ��y��ax+b��
��![]() ����
����![]() ��
��
��y����0.01x+30��
����0.01x+30��x��10x��7500��
��ã�x1��500��x2��1500����ȥ����
�𣺵��ò�Ʒ�����Ϊ500��ʱ������ɻ��7500��Ԫë����
��2����ó��ܻ�õ������۵�ë����Ϊw��Ԫ��
w������0.01x+30��x��10x����0.01��x��1000��2+10000��
��0��x��800��
�൱x��800ʱ��wȡ�����ֵ����ʱw��9600��
�𣺵��ò�Ʒ�����Ϊ800��ʱ���ó��ܻ�õ������۵����ë�������ë������9600��Ԫ��

 �Ķ��쳵ϵ�д�
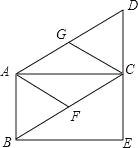
�Ķ��쳵ϵ�д�����Ŀ�����κ���y��ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±����������½��ۣ�
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | 5 | �� |
y | �� | 12 | 5 | 0 | ��3 | ��4 | ��3 | 0 | 5 | 12 | �� |
�ٶ��κ���y��ax2+bx+c����Сֵ����СֵΪ��3���ڵ���![]() ��x��2ʱ��y��0���۶��κ���y��ax2+bx+c��ͼ����x�����������㣬�����Ƿֱ���y������ࣻ�ܵ�x��1ʱ��y��x���������С����������ȷ�����У� ��
��x��2ʱ��y��0���۶��κ���y��ax2+bx+c��ͼ����x�����������㣬�����Ƿֱ���y������ࣻ�ܵ�x��1ʱ��y��x���������С����������ȷ�����У� ��
A. 4�� B. 3�� C. 2�� D. 1��