Question

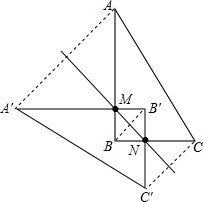
如图，在直角三角形ABC中，∠B=90°，点M、N分别在边BA、BC上，且BM=BN．
（1）画出直角三角形ABC关于直线MN对称的三角形A′B′C′；
（2）如果AB=a，BC=b，BM=x，用a、b、x的代数式分别表示三角形AMA'的面积S₁和四边形AA′C′C的面积S，并化简．

Answer 1

（1）△A′B′C′如图所示；

（2）∵∠B=90°，BM=BN，
∴△BMN是等腰直角三角形，
∴△AMA′是等腰直角三角形，
∴△AMA'的面积S₁=

1

2

（a-x）²=

1

2

a²-ax+

1

2

x²；
四边形AA′C′C的面积S=△AMA′的面积+△CNC′的面积+△ABC的面积+△A′B′C′的面积-正方形BNB′M的面积，
=

1

2

（a-x）²+

1

2

（b-x）²+

1

2

ab+

1

2

ab-x²，
=

1

2

a²+

1

2

b²-ax-bx+ab．