题目内容
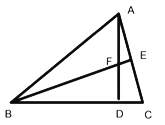
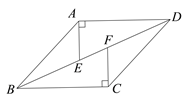
【题目】如图,在菱形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F.
(1)证明:△ADE≌△CBF;
(2)连接AF、CE,四边形AECF是菱形吗?说明理由.
【答案】(1)证明见解析;(2)四边形AECF是菱形,理由见解析.
【解析】分析:(1)根据平行线性质得出∠ADB=∠CBD,求出∠EAD=∠BCF =90°,根据ASA证出△ADE≌△CBF即可;(2)连接AC,由菱形的性质可得AC⊥BD,再由△ADE≌△CBF可得∠AED=∠BFC,再由“对角线互相垂直的平行四边形”即可得到结论..
详解:(1)证明:∵四边形ABCD是菱形,∴AD=BC ,AD∥BC ,∴∠ADB=∠CBD.
∵AE⊥AD ∴∠EAD=![]() , 同理∠BCF=
, 同理∠BCF=![]() .
.
∴∠EAD=∠BCF.
在△AED和△CFB中
∠ADB=∠CBD,AD=BC,∠EAD=∠BCF,
∴△ADE≌△CBF.

(2)四边形AECF是菱形.
连接AC,∵四边形ABCD是菱形,
∴AC⊥BD,即AC⊥EF.
由(1)△ADE≌△CBF,∴AE=CF ,∠AED=∠BFC,∴AE∥CF ,
∴四边形AECF是菱形.

 名师点睛字词句段篇系列答案
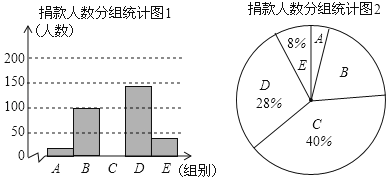
名师点睛字词句段篇系列答案【题目】昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5.
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | 40≤x<50 |
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.