题目内容
【题目】对于有理数a,b,定义两种新运算“※”与“◎”，规定: a※b=a2+2ab,a◎b=|a+ b|-|a- b|,例如，2※(- 1)=22+2×2×(-1)=0,(- 2) ※3=|-2+3|-| - 2-3|= -4.
b c
(1)计算(- 3) ※2的值;
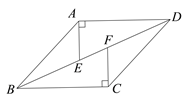
(2)若a, b在数轴上的位置如图所示，化简a◎b;
(3)若(-2) ※x=2◎(- 4)+ 3x,求x的值:
(4)对于任意有理数m,n,请你定义一种新运算“★” ，使得(-3) ★5 = 4,直接写出你定义的运算:m★n=_ (用含m,n的式子表示).
【答案】（1）-3；（2）-2b；（3）
；（4）2（m+n）（答案不唯一）.
【解析】
（1）根据定义新运算公式计算即可；
（2）先判断a+ b和a- b的符号，然后根据绝对值的性质去绝对值化简即可；
（3）根据定义新运算公式解方程即可；
（4）根据已知等式，写出一种使等式成立的新运算即可.
解：（1）根据定义新运算公式可得：(- 3) ※2=（-3）2+2× (-3) ×2=-3；
（2）由数轴可知：a+ b＜0，a－b＜0
∴a◎b=|a+ b|-|a- b|
=- a-b+a-b
=-2b
（3）(-2) ※x=2◎(- 4)+ 3x
（-2）2+2× (-2) x=|2+（-4）|-|2-（-4）|+ 3x
4-4x=-4+ 3x
-7x=-8
解得：x=
（4）∵(-3) ★5 = 4,而2×（-3+5）=4
∴可以定义m★n=2（m+n）
故答案为：2（m+n）（答案不唯一）.
练习册系列答案
名校课堂系列答案
相关题目
