题目内容
【题目】定义:若一个四边形能被其中的一条对角线分割成两个相似三角形,则称这个四边形为“友谊四边形”.我们熟知的平行四边形就是“友谊四边形”,
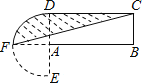
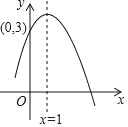
(1)如图1,在4×4的正方形网格中有一个Rt△ABC,请你在网格中找格点D,使得四边形ABCD是被AC分割成的“友谊四边形”,(要求画出点D的2种不同位置)
(2)如图2,BD平分∠ABC,BD=4![]() ,BC=8,四边形ABCD是被BD分割成的“友谊四边形”,求AB长;
,BC=8,四边形ABCD是被BD分割成的“友谊四边形”,求AB长;
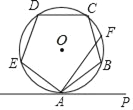
(3)如图3,圆内接四边形ABCD中,∠ABC=60,点E是![]() 的中点,连结BE交CD于点F,连结AF,∠DAF=30°
的中点,连结BE交CD于点F,连结AF,∠DAF=30°
①求证:四边形ABCF是“友谊四边形”;
②若△ABC的面积为6![]() ,求线段BF的长.
,求线段BF的长.
【答案】(1)详见解析;(2)AB=6或8.(3)①详见解析;②2![]()
【解析】
(1)由题意可找到点D位置;
(2)分△ABD∽△CBD,△ABD∽△DBC两种情况讨论,由相似三角形的性质可求AB的长度;
(3)①由题意可得∠ABE=∠EBC=30°,由三角形内角和定理和圆的内接四边形性质可得∠BAF=∠BFC,可证△ABF∽△FBC,即四边形ABCF是“友谊四边形”;
②由相似三角形的性质可得BF2=ABBC,由三角形面积公式可求![]() AB×BC=6
AB×BC=6![]() ,即可求BF的长.
,即可求BF的长.
解:(1)画出点D的2个位置.

(2)∵四边形ABCD为被BD分割的友谊四边形
∴△ABD与△DBC相似,
若△ABD∽△CBD
则![]()
∴AB=BC=8
若△ABD∽△DBC
则![]()
∴AB=![]() =6
=6
综上所述:AB=6或8.
(3)①∵E是![]() 的中点,
的中点,
∴∠ABE=∠CBE=![]() ∠ABC=30°,
∠ABC=30°,
∴∠C+∠BFC=150°,
∵四边形ABCD内接于圆O,
∴∠BAD+∠C=180°,
∵∠DAF=30°,
∴∠C+∠BAF=150°,且∴∠C+∠BFC=150°,
∴∠BAF=∠BFC,且∠ABE=∠CBE
∴△ABF∽△FBC.
∴四边形ABCF为友谊四边形
②如图,过点A作AG⊥BC交BC与G,连接AC,

∵△ABF∽△FBC,
∴![]()
∴BF2=ABBC,
∵S△ABC=![]() BC×AG=
BC×AG=![]() BC×AB×sin60°=6
BC×AB×sin60°=6![]()
∴![]() AB×BC=6
AB×BC=6![]()
∴AB×BC=24=BF2,且BF>0,
∴BF=2![]()

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
【题目】某中学为了了解“校园文明监督岗”的值围情况,对全校各班级进行了抽样调查,过程如下:
收集数据:从三个年级中随机抽取了20个班级,学校对各班的评分如下:
92 71 89 82 69 82 96 83 77 83
80 82 66 73 82 78 92 70 74 59
整理、描述数据:按如下分数段整理、描述这两组样本数据:
分数段 |
|
|
|
|
|
班级数 | 1 | 2 | a | 8 | b |
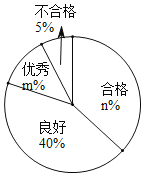
![]() 说明:成绩90分及以上为优秀,
说明:成绩90分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格
分为合格,60分以下为不合格![]()
分析数据:样本数据的平均数、中位数、众数、极差如下表,绘制扇形统计图:
平均数 | 中位数 | 众数 | 极差 |
79 | c | 82 | d |
请根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______.
______.
![]() 若我校共120个班级,估计得分为优秀的班级有多少个?
若我校共120个班级,估计得分为优秀的班级有多少个?
![]() 为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励
为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励![]() 如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由
如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由