题目内容
【题目】在△ABC中，AC= 
，∠A=30°，BC=1，则AB= ．
【答案】1或2
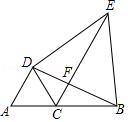
【解析】解：如图1，过点C作CD⊥BA于D，设CD=x， 
∵∠A=30°，
∴AC=2x，AD= 
x，
∵AC= ，
∴x= 
，
∴CD= ，
∴BD= 
，
∴AB=2，
如图2．过B作BD⊥AC于D，
∵∠A=30°，
∴AB= BD，AD= BD，
∴CD= ﹣ BD，
∵BC=1，
在Rt△BCD中，BD2+CD2=BC2 ，
即BD2+（ ﹣ BD）2=12 ，
解得
所以，DB=1或 ．
∴AB=1．或AB=2，
所以答案是：1或2．
【考点精析】通过灵活运用含30度角的直角三角形和勾股定理的概念，掌握在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．
练习册系列答案
相关题目
【题目】某校举行了“文明在我身边”摄影比赛．已知每幅参赛作品成绩记为x分（60≤x≤100）．校方从600幅参赛作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．
“文明在我身边”摄影比赛成绩统计表
分数段 | 频数 | 频率 |
60≤x＜70 | 18 | 0.36 |
70≤x＜80 | 17 | c |
80≤x＜90 | a | 0.24 |
90≤x≤100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题：
（1）统计表中c的值为；样本成绩的中位数落在分数段中；
（2）补全频数分布直方图；
（3）若80分以上（含80分）的作品将被组织展评，试估计全校被展评作品数量是多少？
