题目内容
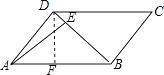
【题目】如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤裁剪和拼图. 
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,BD= , 对角线MN长度的最小值为 .
【答案】![]() ;
;![]()
【解析】解:∵△ABE≌△CDF≌△PMQ, ∴AE=DF=PM,∠EAB=∠FDC=∠MPQ,
∵△ADE≌△BCG≌△PNR,
∴AE=BG=PN,∠DAE=∠CBG=∠RPN,
∴PM=PN,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=45°,
∴∠MPN=90°,
∴△MPN是等腰直角三角形,
当PM最小时,对角线MN最小,即AE取最小值,
∴当AE⊥BD时,AE取最小值,
过D作DF⊥AB于F,
∵平行四边形ABCD的面积为6,AB=3,
∴DF=2,
∵∠DAB=45°,
∴AF=DF=2,
∴BF=1,
∴BD= ![]() =
= ![]() ,
,
∴AE= ![]() =
= ![]() =
= ![]() ,
,
∴MN= ![]() AE=
AE= ![]() .
.
所以答案是: ![]() ,
, ![]() .
.
【考点精析】解答此题的关键在于理解平移的性质的相关知识,掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)每月产销量y(个)与销售单价x(元)之间的函数关系式为; 从上表可知,每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;
(2)若每个玩具的固定成本为30元,求它的销售单价是多少元?
(3)若该厂这种玩具的月产销量不超过400个,求此时销售单价最低为多少元?




