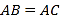题目内容
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() 的平分线
的平分线![]() 与
与![]() 轴相较于点
轴相较于点![]() ,
,![]() 、
、![]() 两点关于
两点关于![]() 轴对称.
轴对称.
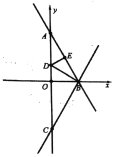
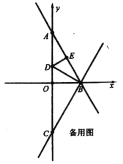
(1)一动点![]() 从点
从点![]() 出发,沿适当的路径运动到直线
出发,沿适当的路径运动到直线![]() 上的点
上的点![]() ,再沿适当的路径运动到点
,再沿适当的路径运动到点![]() 处.当
处.当![]() 的运动路径最短时,求此时点
的运动路径最短时,求此时点![]() 的坐标及点
的坐标及点![]() 所走最短路径的长.
所走最短路径的长.
(2)点![]() 沿直线
沿直线![]() 水平向右运动得点
水平向右运动得点![]() ,平面内是否存在点
,平面内是否存在点![]() 使得以
使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,若存在,请直接写出点
为顶点的四边形为菱形,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)点![]() 的坐标为
的坐标为![]() ,点
,点![]() 所走最短路径的长为
所走最短路径的长为![]() ;(2)存在,点
;(2)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先根据直线的解析式求出点A、B的坐标,再根据直角三角形和角平分线以及对称的性质得出点C、D、E的坐标,然后利用待定系数法可求出直线BC的解析式,最后根据对称性质确定最短路径,求出直线![]() 的解析式,联立两个函数的解析式即可得;
的解析式,联立两个函数的解析式即可得;
(2)根据菱形的性质,分两种情况:BD为边和BD为对角线,然后分别利用菱形的性质、两点之间的距离公式列出等式求解即可.
(1)对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,则点B的坐标为
,则点B的坐标为![]()
当![]() 时,
时,![]() ,则点A的坐标为
,则点A的坐标为![]()
![]() 点
点![]() 为线段
为线段![]() 的中点
的中点
![]()
由点A、B的坐标得:![]()
在![]() 中,
中,![]() ,即
,即![]()
![]()
![]() 平分
平分![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]()
![]()
![]()
![]() 、
、![]() 两点关于
两点关于![]() 轴对称
轴对称
![]()
设直线BC的解析式为![]()
将点![]() 代入得
代入得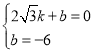 ,解得
,解得
则直线BC的解析式为![]()
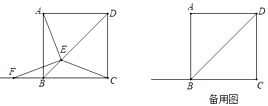
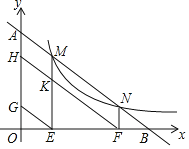
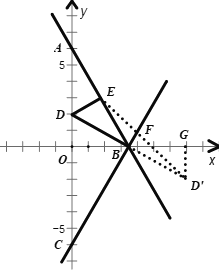
如图,作点D关于直线BC的对称点![]() ,连接ED交BC于点F
,连接ED交BC于点F
由对称的性质、两点之间线段最短可知,点P所走最短路径的长为![]() 的长
的长
由对称的性质可知,![]()
过点![]() 作
作![]() 轴于点G
轴于点G
在![]() 和
和![]() 中,
中,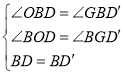
![]()
![]()
![]()
![]()
由两点之间的距离公式得:![]()
设直线![]() 的解析式为
的解析式为![]()
将点![]() 代入得
代入得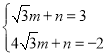 ,解得
,解得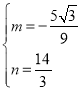
则直线![]() 的解析式为
的解析式为![]()
联立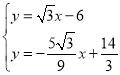 ,解得
,解得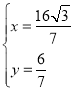
则点![]() 的坐标为
的坐标为![]() ;
;
(2)存在,点![]() 的坐标的求解过程如下:
的坐标的求解过程如下:
![]() ,点
,点![]() 沿直线
沿直线![]() 水平向右运动得点
水平向右运动得点![]()
![]() 可设点
可设点![]() 的坐标为
的坐标为![]() ,且
,且![]()
由菱形的性质,分以下两种情况:
①若BD为边
由菱形的定义得:![]()
由两点之间的距离公式得:![]()
解得![]() 或
或![]() (舍去)
(舍去)
则点![]() 的坐标为
的坐标为![]()
②若BD为对角线
由菱形的定义得:![]()
由两点之间的距离公式得:![]()
解得![]()
则点![]() 的坐标为
的坐标为![]()
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

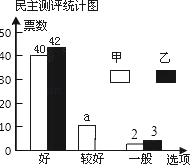
【题目】在校园歌手大赛中,甲、乙两位同学的表现分外突出,现场A、B、C、D、E、F六位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:(说明:随机抽取的50名同学每人必须从“好”、“较好”、“一般”中选一票投给每个选手)
A | B | C | D | E | F | |
甲 | 89 | 97 | 90 | 93 | 95 | 94 |
乙 | 89 | 92 | 90 | 97 | 94 | 94 |
(1)a= ,六位评委对乙同学所打分数的中位数是 ,并补全条形统计图;
(2)学校规定评分标准如下:去掉评委评分中最高和最低分,再算平均分并将平均分与民意测评分按2:3计算最后得分.求甲、乙两位同学的最后得分.(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)