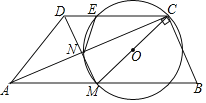
��Ŀ����
����Ŀ����У���ִ����У��ס�����λͬѧ�ı��ַ���ͻ�����ֳ�A��B��C��D��E��F��λ��ί�Ĵ������Լ������ȡ��50��ͬѧ������������ֱ�����ͳ�Ʊ��Ͳ�����������ͳ��ͼ����˵���������ȡ��50��ͬѧÿ�˱���������������Ϻ�������һ������ѡһƱͶ��ÿ��ѡ�֣�
A | B | C | D | E | F | |
�� | 89 | 97 | 90 | 93 | 95 | 94 |
�� | 89 | 92 | 90 | 97 | 94 | 94 |
��1��a���� ������λ��ί����ͬѧ�����������λ������ ��������ȫ����ͳ��ͼ��
��2��ѧУ�涨���ֱ����£�ȥ����ί��������ߺ���ͷ֣�����ƽ���ֲ���ƽ��������������ְ�2��3�������÷֣���ס�����λͬѧ�����÷֣�����������֣�������Ʊ����2+���Ϻ���Ʊ����1+��һ����Ʊ����0��
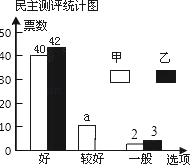
���𰸡���1��8��93 ����������2����ͬѧ�����յ÷�90���֣�����ͬѧ�����յ÷�Ϊ90.4���֣�
��������
��1�����ͳ��ͼ��ͶƱ���������ɵó�![]() ��������λ���Ķ��壬���Ƚ�������С�������У�Ȼ����⼴�ɣ�����ͶƱ������ͳ��ͼ�����������ͬѧ����Ϊ���Ϻ�������������ȫͳ��ͼ���ɣ�
��������λ���Ķ��壬���Ƚ�������С�������У�Ȼ����⼴�ɣ�����ͶƱ������ͳ��ͼ�����������ͬѧ����Ϊ���Ϻ�������������ȫͳ��ͼ���ɣ�
��2������ƽ��������ʽ��⼴�ɣ�Ȼ�ɵó����յ÷�.
��1���������⣬��![]() =50����40+2��=8��
=50����40+2��=8��
��λ��ί����ͬѧ���������С��������Ϊ��89��90��92��94��94��97��
����λ��ί����ͬѧ�����������λ����![]() =93���֣���
=93���֣���
��������ж���ͬѧ����Ϊ���Ϻ���������Ϊ50����42+3��=5���ˣ���
��ȫ����ͼ���£�
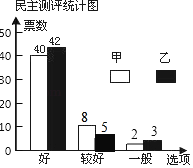
��2����ί�Լ����ֵ�ƽ����Ϊ![]() =93���֣�����ί�������ֵ�ƽ����Ϊ
=93���֣�����ί�������ֵ�ƽ����Ϊ![]() =92.5���֣���
=92.5���֣���
����������Ϊ40��2+8��1+2��0=88���֣����ҵ���������Ϊ42��2+5��1+3��0=89���֣���
���ͬѧ�����յ÷�Ϊ![]() =90���֣�����ͬѧ�����յ÷�Ϊ
=90���֣�����ͬѧ�����յ÷�Ϊ![]() =90.4���֣���
=90.4���֣���

 ÿ��10���ӿ�����������������ϵ�д�
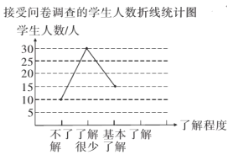
ÿ��10���ӿ�����������������ϵ�д�����Ŀ��Ϊ�᳹��ʵʡ���������������������������ĸ������֮�ʣ�ijУ��ί��֯�������䰮������
ѧ�����棬�ж���ĸ��Ϊ����Ľ��������ѧУ���������50��ͬѧƽ��ÿ���ڼ��������ʱ�䣬ͳ
�Ʋ����������µ�Ƶ���ֲ���������ͳ��ͼ��
��� | �������ʱ�� | Ƶ�� | Ƶ�� |
A | 1��t��2 | 3 | 0.06 |
B | 2��t��4 | 20 | 0.40 |
C | 4��t��6 | a | 0.30 |
D | 6��t��8 | 8 | b |
E | t��8 | 4 | 0.08 |
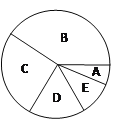
����������Ϣ�ش��������⣺
��1��a= ��b= ��
��2��������ͳ��ͼ�У�B����ռԲ�ĽǵĶ���Ϊ ��
��3��ȫУ����2000��ѧ�������Ƹ�Уƽ��ÿ��������ʱ�䲻����4Сʱ��ѧ��Լ�ж����ˣ�