题目内容
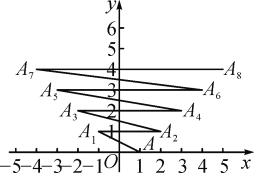
【题目】如图，分别过反比例函数y＝ 
的图象上的点P1(1，y1)，P2(2，y2)，…Pn(n，yn)…作x轴的垂线，垂足分别为A1 ， A2 ， …，An…，连接A1P2 ， A2P3 ， …,An-1Pn ， …，再以A1P1 ， A1P2为一组邻边画一个平行四边形A1P1B1P2 ， 以A 2P2 ， A2P3为一组邻边画一个平行四边形A2P2B2P3 ， 点B2的纵坐标是.依此类推，则点Bn的纵坐标是.(结果用含n代数式表示)
【答案】
；
【解析】∵点P1(1，y1),P2(2，y2)在反比例函数 
的图象上，
∴y1=3,y2= 
；
∴P1A1=y1=3；
又∵四边形A1P1B1P2，是平行四边形，
∴P1A1=B1P2=3，P1A1∥B1P2，
∴点B1的纵坐标是：y2+y1= +3,即点B1的纵坐标是 
；
同理求得,点B2的纵坐标是：y3+y2=1+ = ；
点B3的纵坐标是：y4+y3= 
+1= 
；
…
点Bn的纵坐标是：yn+1+yn= 
；
故答案是 。
由点P1(1，y1)，P2(2，y2)在反比例函数的图象上，求出y1，y2的值，又四边形A1P1B1P2是平行四边形，得到对边平行且相等，求出B1的纵坐标，同理求得,点B2的纵坐标···，得到点Bn的纵坐标.
【题目】某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
（注：获利＝售价－进价）
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元?
