题目内容
【题目】已知，△ABC为等边三角形，点D，E为直线BC上两动点，且BD=CE．点F，点E关于直线AC成轴对称，连接AE，顺次连接AD，DF，AF．
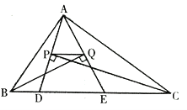
（1）如图1，若点D、点E在边BC上，试判断∠BAD与∠FDC的大小关系，并说明理由；
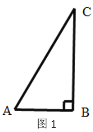
（2）若点D、点E在边BC所在的直线上如图（2）所示的位置，（1）中的结论是否还成立，说明理由．
【答案】（1）
，理由见解析；（2）成立，
，理由见解析．
【解析】
（1）根据等边三角形的性质与判定和全等三角形的判定和性质解答即可；
（2）根据全等三角形的判定和性质以及等边三角形的判定解答即可．
（1），理由如下：
∵
为等边三角形，
∴
，
∵
，
∴
∴
，
，
∵点
，点
关于直线
成轴对称，
∴
，
，
∴
，
，
∵
，
∴
，，
∴
为等边三角形；
∴
∵
又∵
∴
（2）
∵理由：为等边三角形，
∴，
，
∴
∵
∴
∴
，
，
∵点，点关于直线成轴对称，
∴，，
∴，，
∵
，
∴
，∵，
∴为等边三角形，
∴
，
∵
，
∴．
练习册系列答案
相关题目
【题目】某工地因道路建设需要开挖土石方，计划每小时挖掘土石方540m3，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如表：
租金（单位：元/台时） | 挖掘土石方量（单位：m3/台时） | |
甲型机 | 100 | 60 |
乙型机 | 120 | 80 |
（1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型的挖掘机各需多少台？
（2）如果每小时支付的租金不超过850元，又恰好完成每小时的挖掘量，那么共有几种不同的租用方案．
