ΧβΡΩΡΎ»ί
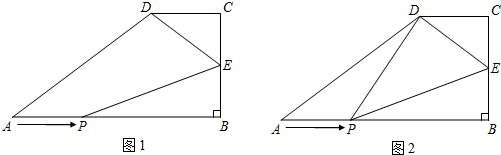
»γΆΦ1Θ§÷±Ϋ«Χί–ΈABCD÷–Θ§ABΓΈCDΘ§ΓœB=90?Θ§AD=10Θ§CD=4Θ§BC=6Θ§E «BCΒΡ÷–ΒψΘ§Ε·ΒψP¥”ΒψA≥ωΖΔΘ§―Ί±ΏAB“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψB‘ΥΕ·Θ§…ηΕ·ΒψP‘ΥΕ·ΒΡ ±ΦδΈΣtΟκΘ°
Θ®1Θ©«σœΏΕΈABΒΡ≥ΛΘΜ
Θ®2Θ©Β±ΓςPBE”κΓςDCEœύΥΤ ±Θ§«σtΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦ2Θ§Ν§Ϋ”PDΘ§“‘PDΥυ‘Ύ÷±œΏΈΣΕ‘≥Τ÷αΉςœΏΕΈBCΒΡ÷αΕ‘≥ΤΆΦ–ΈBΓδCΓδΘ§»τΒψCΓδ¬δ‘ΎœΏΕΈAD…œΘ§‘ρtΒΡ÷ΒΈΣ
Θ®1Θ©«σœΏΕΈABΒΡ≥ΛΘΜ
Θ®2Θ©Β±ΓςPBE”κΓςDCEœύΥΤ ±Θ§«σtΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦ2Θ§Ν§Ϋ”PDΘ§“‘PDΥυ‘Ύ÷±œΏΈΣΕ‘≥Τ÷αΉςœΏΕΈBCΒΡ÷αΕ‘≥ΤΆΦ–ΈBΓδCΓδΘ§»τΒψCΓδ¬δ‘ΎœΏΕΈAD…œΘ§‘ρtΒΡ÷ΒΈΣ
10
10
Θ®÷±Ϋ”–¥≥ω¥πΑΗΦ¥Ω…Θ©Θ°
Ζ÷ΈωΘΚΘ®1Θ©ΉςDFΓΆAB”ΎFΘ§ΗυΨί“―÷ΣΧθΦΰΩ…“‘ΒΟ≥ωΥΡ±Ώ–ΈBCDF «ΨΊ–ΈΨΆΩ…“‘ΒΟ≥ωBF=CDΘ§‘Ό”…Ι¥Ι…Ε®άμ«σ≥ωAFΒΡ÷ΒΨΆΩ…“‘ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©¥”ΓςPBEΓΉΓςDCEΚΆΓςPBEΓΉΓςECDΝΫ÷÷«ιΩωΫχ––Χ÷¬έΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΨΆΩ…“‘ΒΟ≥ωΫα¬έ«σ≥ωtΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦ4Θ§ΗυΨί÷αΕ‘≥ΤΒΡ–‘÷ œ»«σ≥ωACΓδΒΡ÷ΒΘ§‘Ό”…»ΐΫ«Κ· ΐ÷Β«σ≥ωGCΓδΘ§AGΒΡ÷ΒΘ§‘Ό÷ΛΟςΓςACΓδGΓΉΓςPBΓδGΘ§”…œύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΨΆΩ…“‘«σ≥ωPGΒΡ÷ΒΘ§¥”Εχ«σ≥ωAPΒΡ÷ΒΨΆΩ…“‘«σ≥ωtΒΡ÷ΒΘ°
Θ®2Θ©¥”ΓςPBEΓΉΓςDCEΚΆΓςPBEΓΉΓςECDΝΫ÷÷«ιΩωΫχ––Χ÷¬έΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΨΆΩ…“‘ΒΟ≥ωΫα¬έ«σ≥ωtΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦ4Θ§ΗυΨί÷αΕ‘≥ΤΒΡ–‘÷ œ»«σ≥ωACΓδΒΡ÷ΒΘ§‘Ό”…»ΐΫ«Κ· ΐ÷Β«σ≥ωGCΓδΘ§AGΒΡ÷ΒΘ§‘Ό÷ΛΟςΓςACΓδGΓΉΓςPBΓδGΘ§”…œύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΨΆΩ…“‘«σ≥ωPGΒΡ÷ΒΘ§¥”Εχ«σ≥ωAPΒΡ÷ΒΨΆΩ…“‘«σ≥ωtΒΡ÷ΒΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©»γΆΦ1Θ§ΉςDFΓΆAB”ΎFΘ§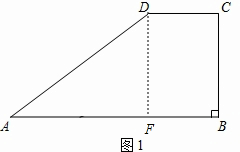
ΓύΓœAFD=ΓœBFD=90ΓψΘ°
ΓΏABΓΈCDΘ§ΓœB=90ΓψΘ§
ΓύΓœC=90ΓψΘ§
ΓύΥΡ±Ώ–ΈBCDF «ΨΊ–ΈΘ§
ΓύBF=CDΘ§DF=BCΘ°
ΓΏCD=4Θ§BC=6Θ§
ΓύBF=4Θ§DF=6Θ°
‘ΎRtΓςAFD÷–Θ§”…Ι¥Ι…Ε®άμΘ§ΒΟ
AF=
=8Θ°
ΓύAB=4+8=12Θ°
Θ®2Θ©»γΆΦ2Θ§Β±P‘ΥΕ·tΟκ ±Θ§ΓςPBEΓΉΓςDCE
Γύ
=
Θ°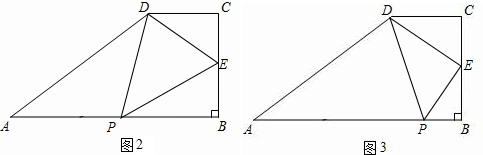
ÿAP=tȧ
ΓύBP=12-tΘ°
ΓΏE «BCΒΡ÷–ΒψΘ§
ΓύCE=BE=3Θ°
Γύ
=
Θ§
Γύt=8ΘΜ
»γΆΦ3Θ§Β±P‘ΥΕ·tΟκ ±Θ§ΓςPBEΓΉΓςECDΘ§
Γύ
=
Γύ
=
Θ§
Γύt=
Θ°
ΓύtΒΡ÷ΒΈΣ8Μρ
ΘΜ
Θ®3Θ©»γΆΦ4Θ§ΉςCBΙΊ”ΎPDΒΡ÷αΕ‘≥ΤΆΦ–ΈCΓδBΓδΫΜAB”ΎΒψGΘ§Ν§Ϋ”PBΓδΘ§
ΓύΓœDCΓδBΓδ=ΓœC=90ΓψΘ§ΓœBΓδ=ΓœB=90ΓψΘ§CΓδD=CD=4Θ§PBΓδ=PBΘ°
ΓύACΓδ=6Θ§
»γΆΦ1Θ§‘ΎRtΓςAFD÷–Θ§AD=10Θ§DF=6Θ§AF=8Θ§
tanΓœA=
Θ§cosΓœA=
Θ°
‘ΎRtΓςACΓδG÷–Θ§
tanΓœA=
=
Θ§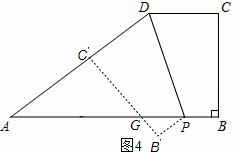
Γύ
=
Θ§
ΓύGCΓδ=
Θ§
cosΓœA=
=
Θ§
Γύ
=
Θ§
ΓύAG=
Θ§
ΓύGP=t-
Θ§PB=PBΓδ=12-tΘ§
ΓΏΓςACΓδGΓΉΓςPBΓδGΘ§
Γύ
=
Θ§
Γύ
=
Θ§
Γύt=10Θ°
Ι ¥πΑΗΈΣΘΚ10Θ°

ΓύΓœAFD=ΓœBFD=90ΓψΘ°
ΓΏABΓΈCDΘ§ΓœB=90ΓψΘ§
ΓύΓœC=90ΓψΘ§
ΓύΥΡ±Ώ–ΈBCDF «ΨΊ–ΈΘ§
ΓύBF=CDΘ§DF=BCΘ°
ΓΏCD=4Θ§BC=6Θ§
ΓύBF=4Θ§DF=6Θ°
‘ΎRtΓςAFD÷–Θ§”…Ι¥Ι…Ε®άμΘ§ΒΟ
AF=
| 100-36 |
ΓύAB=4+8=12Θ°
Θ®2Θ©»γΆΦ2Θ§Β±P‘ΥΕ·tΟκ ±Θ§ΓςPBEΓΉΓςDCE
Γύ
| PB |
| DC |
| BE |
| CE |

ÿAP=tȧ
ΓύBP=12-tΘ°
ΓΏE «BCΒΡ÷–ΒψΘ§
ΓύCE=BE=3Θ°
Γύ
| 12-t |
| 4 |
| 3 |
| 3 |
Γύt=8ΘΜ
»γΆΦ3Θ§Β±P‘ΥΕ·tΟκ ±Θ§ΓςPBEΓΉΓςECDΘ§
Γύ
| PB |
| EC |
| BE |
| CD |
Γύ
| 12-t |
| 3 |
| 3 |
| 4 |
Γύt=
| 39 |
| 4 |
ΓύtΒΡ÷ΒΈΣ8Μρ
| 39 |
| 4 |
Θ®3Θ©»γΆΦ4Θ§ΉςCBΙΊ”ΎPDΒΡ÷αΕ‘≥ΤΆΦ–ΈCΓδBΓδΫΜAB”ΎΒψGΘ§Ν§Ϋ”PBΓδΘ§
ΓύΓœDCΓδBΓδ=ΓœC=90ΓψΘ§ΓœBΓδ=ΓœB=90ΓψΘ§CΓδD=CD=4Θ§PBΓδ=PBΘ°
ΓύACΓδ=6Θ§
»γΆΦ1Θ§‘ΎRtΓςAFD÷–Θ§AD=10Θ§DF=6Θ§AF=8Θ§
tanΓœA=
| 3 |
| 4 |
| 4 |
| 5 |
‘ΎRtΓςACΓδG÷–Θ§
tanΓœA=
| GCΓδ |
| ACΓδ |
| 3 |
| 4 |

Γύ
| GCΓδ |
| 6 |
| 3 |
| 4 |
ΓύGCΓδ=
| 9 |
| 2 |
cosΓœA=
| ACΓδ |
| AG |
| 4 |
| 5 |
Γύ
| 6 |
| AG |
| 4 |
| 5 |
ΓύAG=
| 15 |
| 2 |
ΓύGP=t-
| 15 |
| 2 |
ΓΏΓςACΓδGΓΉΓςPBΓδGΘ§
Γύ
| AG |
| PG |
| ACΓδ |
| PBΓδ |
Γύ
| ||
t-
|
| 6 |
| 12-t |
Γύt=10Θ°
Ι ¥πΑΗΈΣΘΚ10Θ°
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥ÷±Ϋ«Χί–ΈΒΡ–‘÷ Θ§Ι¥Ι…Ε®άμΒΡ‘Υ”ΟΘ§÷αΕ‘≥ΤΒΡ–‘÷ ΒΡ‘Υ”ΟΘ§œύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®ΦΑ–‘÷ ΒΡ‘Υ”ΟΘ§‘ΎΫβ¥π ±÷ΛΟς»ΐΫ«–ΈœύΥΤ «ΙΊΦϋΘ§‘Υ”Ο»ΐΫ«–ΈœύΥΤΒΡ–‘÷ «σœΏΕΈΒΡ≥Λ «÷ΊΒψΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ΜΣΕΪ Π¥σΑφ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
ΜΣΕΪ Π¥σΑφ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
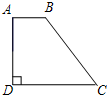 »γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ABΓΈDCΘ§ΓœD=90ΓψΘ§»τAD=8Θ§BC=10Θ§‘ρcosCΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ABΓΈDCΘ§ΓœD=90ΓψΘ§»τAD=8Θ§BC=10Θ§‘ρcosCΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©AΓΔ
| ||
BΓΔ
| ||
CΓΔ
| ||
DΓΔ
|
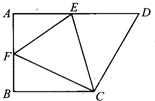 12ΓΔ»γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœB=90ΓψΘ§ΫΪ÷±Ϋ«Χί–ΈABCD―ΊCE’έΒΰΘ§ ΙΒψD¬δ‘ΎAB…œΒΡFΒψΘ§»τAB=BC=12Θ§EF=10Θ§ΓœFCD=90ΓψΘ§‘ρAF=
12ΓΔ»γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœB=90ΓψΘ§ΫΪ÷±Ϋ«Χί–ΈABCD―ΊCE’έΒΰΘ§ ΙΒψD¬δ‘ΎAB…œΒΡFΒψΘ§»τAB=BC=12Θ§EF=10Θ§ΓœFCD=90ΓψΘ§‘ρAF= ΈΣtΘ®ΒΞΈΜΘΚΟκΘ©Θ°
ΈΣtΘ®ΒΞΈΜΘΚΟκΘ©Θ° Θ®2013•ΚΎΝζΫ≠Θ©»γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœBCD=90ΓψΘ§ΓœABC=45ΓψΘ§AD=CDΘ§CEΤΫΖ÷ΓœACBΫΜAB”ΎΒψEΘ§‘ΎBC…œΫΊ»ΓBF=AEΘ§Ν§Ϋ”AFΫΜCE”ΎΒψGΘ§Ν§Ϋ”DGΫΜAC”ΎΒψHΘ§ΙΐΒψAΉςANΓΆBCΘ§¥ΙΉψΈΣNΘ§ANΫΜCE”ΎΒψMΘ°‘ρœ¬Ν–Ϋα¬έΘΜΔΌCM=AFΘΜΔΎCEΓΆAFΘΜΔέΓςABFΓΉΓςDAHΘΜΔήGDΤΫΖ÷ΓœAGCΘ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ®ΓΓΓΓΘ©
Θ®2013•ΚΎΝζΫ≠Θ©»γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœBCD=90ΓψΘ§ΓœABC=45ΓψΘ§AD=CDΘ§CEΤΫΖ÷ΓœACBΫΜAB”ΎΒψEΘ§‘ΎBC…œΫΊ»ΓBF=AEΘ§Ν§Ϋ”AFΫΜCE”ΎΒψGΘ§Ν§Ϋ”DGΫΜAC”ΎΒψHΘ§ΙΐΒψAΉςANΓΆBCΘ§¥ΙΉψΈΣNΘ§ANΫΜCE”ΎΒψMΘ°‘ρœ¬Ν–Ϋα¬έΘΜΔΌCM=AFΘΜΔΎCEΓΆAFΘΜΔέΓςABFΓΉΓςDAHΘΜΔήGDΤΫΖ÷ΓœAGCΘ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ®ΓΓΓΓΘ© »γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœD=90ΓψΘ§AD=aΘ§BC=bΘ§AB=cΘ§“‘ABΈΣ÷±ΨΕΉςΓ―OΘ° ‘ΧΫΨΩΘΚ
»γΆΦΘ§‘Ύ÷±Ϋ«Χί–ΈABCD÷–Θ§ADΓΈBCΘ§ΓœD=90ΓψΘ§AD=aΘ§BC=bΘ§AB=cΘ§“‘ABΈΣ÷±ΨΕΉςΓ―OΘ° ‘ΧΫΨΩΘΚ