题目内容
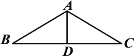
【题目】如图,点![]() 在⊙
在⊙![]() 的直径
的直径![]() 的延长线上,点
的延长线上,点![]() 在⊙
在⊙![]() 上,
上, ![]() ,
, ![]() .
.
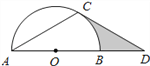
(1)求证: ![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若⊙![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;
(2)先根据直角三角形中30°的锐角所对的直角边是斜边的一半求出OD,然后根据勾股定理求出CD,则阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.
(1)证明:连接OC.

∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=∠ACD-∠2=90°,
即OC⊥CD,
∴CD是⊙O的切线;
(2)解:∠1=∠2+∠A=60°.
∴S扇形BOC=![]() =
=![]() .
.
在Rt△OCD中,∠D=30°,
∴OD=2OC=4,
∴CD=![]() =
=![]() .
.
∴SRt△OCD=![]() OC×CD=
OC×CD=![]() ×2×
×2×![]() =
=![]() .
.
∴图中阴影部分的面积为: ![]() -
-![]() .
.

练习册系列答案
相关题目
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
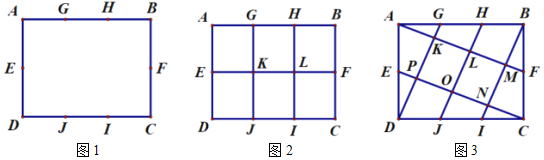
图形 |
|
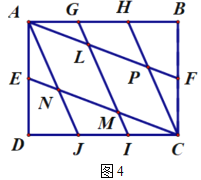
|
| … |
我们把某格中字母和所得到的多项式称为“特征多项式”,例如第1格的“特征多项式”为![]() .
.
回答下列问题:
(1)第3格的“特征多项式”为____________,
第4格的“特征多项式”为____________,
第![]() 格的“特征多项式”为____________;
格的“特征多项式”为____________;
(2)若第1格的“特征多项式”的值为10,第2格的“特征多项式”的值为19,求![]() 的值.
的值.