��Ŀ����
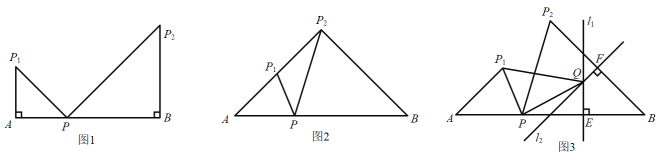
����Ŀ������ƽ��ֱ������ϵxOy�еĶ���P��ͼ��F���������¶��壺����ͼ��F�ϴ���һ��N��ʹ�õ�Q����P����ֱ��ON�Գƣ���Ƶ�Q�ǵ�P����ͼ��F�Ķ���ԳƵ㣮
��1����ͼ��![]() ��
��![]() ��
��![]() ��
��

����P���ڵ�B�Ķ���ԳƵ�������� ��
���ڵ�![]() ��
��![]() ��
��![]() �У�______�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
�У�______�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
��2��ֱ��![]() �ֱ���x�ᣬy�ύ�ڵ�G��H����M���Ե�
�ֱ���x�ᣬy�ύ�ڵ�G��H����M���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ��
Ϊ�뾶��Բ��
����![]() ʱ������M�ϴ��ڵ�K��ʹ���������߶�GH�Ķ���ԳƵ����߶�GH�ϣ���
ʱ������M�ϴ��ڵ�K��ʹ���������߶�GH�Ķ���ԳƵ����߶�GH�ϣ���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ����
����![]() ʱ�����߶�GH�ϴ��ڵ�J��ʹ����������M�Ķ���ԳƵ�����M�ϣ�ֱ��д��b��ȡֵ��Χ��
ʱ�����߶�GH�ϴ��ڵ�J��ʹ����������M�Ķ���ԳƵ�����M�ϣ�ֱ��д��b��ȡֵ��Χ��
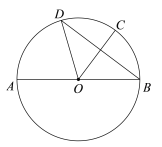
���𰸡���1����![]() ������C��D����2����
������C��D����2����![]() ��
��![]() ����
����![]() ��
��
��������
��1���������P����ֱ��OB�ĶԳƵ�G���ɣ�
�����OP��OC��OD��OE�ij������жϣ�
��2���������������λ��b��ֵ���ɣ���ͼ2�У�����M����y��ĶԳ�ͼ����M�䣬��ֱ��GH����M���ڵ�һ��������ʱ�����е�ΪP������PM�䣮��ͼ3�У���OΪԲ�ģ�3Ϊ�뾶����O����ֱ��GH����O�ڵ������������ڵ�Pʱ������OP���ֱ����OH��ֵ���ɽ�����⣮
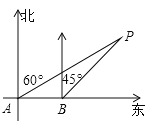
����ͼ4�У�����M��x����K��T����K����1��0����T��5��0���������������λ��b��ֵ�����жϣ�
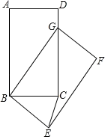
�⣺��1������ͼ1�У�
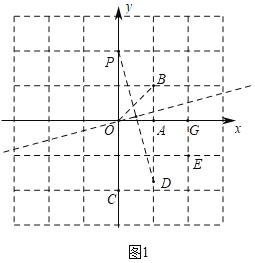
��P��0��2����B��1��1����
���P����OB�ĶԳƵ�G��2��0����
�ʴ�Ϊ����2��0����
���ߵ�C��0����2����D��1����![]() ����E��2����1����
����E��2����1����
��OP��2��OD��2��OC��2��OE��![]() ��
��
��OP��OD��OC��
���C��D�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
�ʴ�Ϊ����C��D��
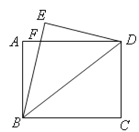
��2������ͼ2�У�����M����y��ĶԳ�ͼ����M�䣬��ֱ��GH����M���ڵ�һ��������ʱ�����е�ΪP������PM�䣬
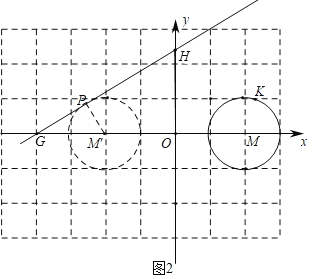
��b��0ʱ��
������ã�tan��HGO��![]() ��
��
���PGM��30�㣬
��PM�䣽1����MPG��90�㣬
��MG��2MP��2��
��OG��GM+OM��4��
��OH��OGtan30�㣽![]() ��
��
��ֱ�߾�����-1��0��ʱ��![]() .
.
��![]()
��b��0ʱ��
����ֱ�߾�����1��0��ʱ��![]() .
.
��ͼ3�У���OΪԲ�ģ�3Ϊ�뾶����O����ֱ��GH��
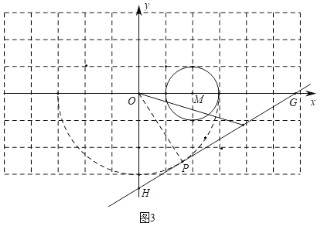
ͬ���ɵ�OH��2![]() ����
����![]()
�۲�ͼ���֪����������b��ֵ����2![]() ��b��
��b��![]() ��
��
����������b��ȡֵ��Χ��![]() ��
��![]() .
.
����ͼ4�У�����M��x����K��T����K����1��0����T��5��0����
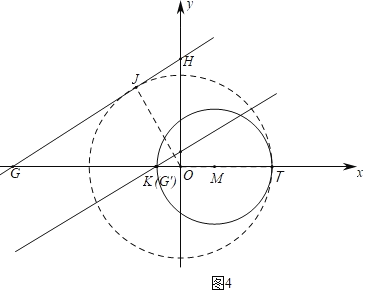
��OΪԲ�ģ�5Ϊ�뾶����O����ֱ��GH����O�ڵڶ����������ڵ�Jʱ��
�ɵ�OH��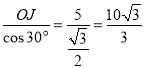 ��
��
��ʱֱ��GH�Ľ���ʽΪy��![]() x+
x+![]() ��
��
��ֱ��GH������K����1��0��ʱ��0����![]() +b��
+b��
�ɵ�b��![]() ��
��
��ʱֱ��GH�Ľ���ʽΪy��![]() x+
x+![]() ��
��
�۲�ͼ���֪����������b��ֵΪ��![]() ��b��
��b��![]() ��
��

 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�