题目内容
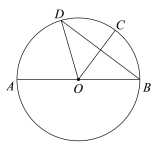
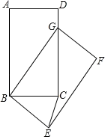
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 按顺时针方向旋转得到矩形
按顺时针方向旋转得到矩形![]() ,点
,点![]() 落在矩形
落在矩形![]() 的边
的边![]() 上的点
上的点![]() 处,连接
处,连接![]() ,则点
,则点![]() 到
到![]() 的距离是( )
的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接AG,过点B作BH⊥CE,垂足为点H,根据旋转变换的性质得到∠ABG=∠CBE,BA=BG,根据勾股定理求出CG、AD,根据相似三角形的性质列出比例式,计算即可得到CE,再根据等腰三角形的三线合一即可得到CH的长,最后根据勾股定理即可求得答案.
解:连接AG,过点B作BH⊥CE,垂足为点H,
∵在矩形ABCD中,
∴CD=AB=5,AD=BC=3,∠BCD=∠D=90°,
∵旋转,
∴∠ABG=∠CBE,BA=BG=5,BC=BE,
∴在Rt△BCG中,CG=![]() =4,
=4,
∴DG=DC﹣CG=1,
∴在Rt△ADG中,AG=![]() =
=![]() ,
,
∵![]() =
=![]() ,∠ABG=∠CBE,
,∠ABG=∠CBE,
∴△ABG∽△CBE,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得,CE=![]() ,
,
∵BC=BE,BH⊥CE,
∴CH=EH=![]() CE=
CE=![]() ,∠BHC=90°,
,∠BHC=90°,
∴在Rt△BCH中,BH=![]() =
=![]() ,
,
故选:A.

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】某初中学校每个年级学生刚好为500人,为了解数学史知识的普及情况,随机从每个年级各抽10名学生进行测试,测试成绩整理如下:
年级 | 学生测试成绩表 | |||||||||
七年级 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
八年级 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
九年级 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求每个年级恰好都有一名学生参加的概率.
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
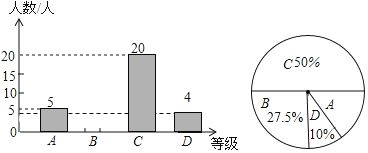
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?