Question

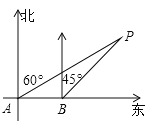
【题目】如图，大海中某灯塔P周围10海里范围内有暗礁，一艘海轮在点A处观察灯塔P在北偏东60°方向，该海轮向正东方向航行8海里到达点B处，这时观察灯塔P恰好在北偏东45°方向．如果海轮继续向正东方向航行，会有触礁的危险吗？试说明理由．（参考数据：≈1.73）

Answer 1

【答案】没有触礁的危险．

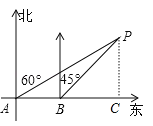
【解析】试题分析：作PC⊥AB于C，如图，∠PAC=30°，∠PBC=45°，AB=8，设PC=x，先判断△PBC为等腰直角三角形得到BC=PC=x，再在Rt△PAC中利用正切的定义列方程，求出x的值，即得到AC的值，然后比较AC与10的大小即可判断海轮继续向正东方向航行，是否有触礁的危险．

试题解析：没有触礁的危险．理由如下：

作PC⊥AB于C，如图，∠PAC=30°，∠PBC=45°，AB=8，设PC=x，在Rt△PBC中，∵∠PBC=45°，∴△PBC为等腰直角三角形，∴BC=PC=x，在Rt△PAC中，∵tan∠PAC=，∴AC=，即8+x=，解得x=≈10.92，即AC≈10.92，∵10.92＞10，∴海轮继续向正东方向航行，没有触礁的危险．