Question

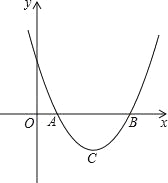
【题目】设二次函数y=ax2+bx+c（a＞0）的图象与x轴的两个交点A（x1，0），B（x2，0），抛物线的顶点为C，显然△ABC为等腰三角形．

（1）当△ABC为等腰直角三角形时，求b2﹣4ac的值；

（2）当△ABC为等边三角形时，求b2﹣4ac的值．

Answer 1

【答案】(1)、4；(2)、12

【解析】

试题分析：(1)、由于抛物线与x轴有两个不同的交点，所以b2﹣4ac＞0；可求得线段AB的表达式，利用公式法可得到顶点C的纵坐标，进而求得斜边AB上的高（设为CD），若△ABC为等腰直角三角形，那么AB=2CD，可根据这个等量关系求出b2﹣4ac的值；(2)、当△ABC为等边三角形时，解直角△ACE，得CE=AE=AB，据此列出方程，解方程求出b2﹣4ac的值．

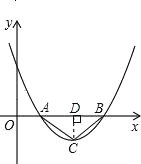
试题解析：(1)、当△ABC为等腰直角三角形时，过C作CD⊥AB于D，则AB=2CD；

∵抛物线与x轴有两个交点， ∴△＞0， ∴|b2﹣4ac|=b2﹣4ac， ∵AB=，

又∵CD=（a≠0）， ∴， ∴b2﹣4ac=，

∵b2﹣4ac≠0， ∴b2﹣4ac=4．

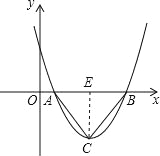
(2)、如图，当△ABC为等边三角形时， 由（1）可知CE=AE=AB，

∴， ∵b2﹣4ac＞0， ∴， ∴b2﹣4ac=12．