题目内容
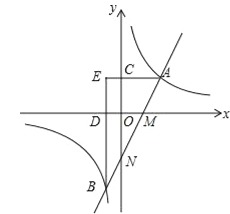
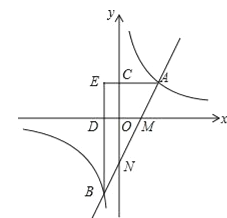
【题目】如图，直线y=2x﹣2分别与x轴、y轴相交于M，N两点，并且与双曲线y=
（k＞0）相交于A，B两点，过点A作AC⊥y轴于点C，过点B作BD⊥x轴于点D，AC与BD的延长线交于点E（m，n）．
（1）求证：
；
（2）若
，求
＞2x﹣2的x的取值范围；
（3）在（2）的条件下，P为双曲线上一点，以OB，OP为邻边作平行四边形，且平行四边形的周长最小，求第四个顶点Q的坐标．
【答案】(1)、证明过程见解析；(2)、x＜﹣1或0＜x＜2；(3)、P（2，2）或（﹣2，﹣2），Q（1，﹣2）或（﹣3，﹣6）．
【解析】
试题分析：(1)、设A（x1，
），B（x2，
），则有AE=x1﹣x2，BE=
﹣
，EC=﹣x2，ED=，首先证明
=
，由此即可解决问题．(2)、由DM∥AE，得
=
=
，设A（m，n）则B（﹣
，﹣2n），把A、B代入y=2x﹣2得到：
，解得：
，求出A、B两点坐标即可解决问题．(3)、因为点B是定点，OB是定长，所以要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可，由P在y=
上，设P（a，
），因为OP2=n2+
=（n﹣
）2+8，所以当n﹣
=0时，OP2的值最小，由此即可解决问题．
试题解析：(1)、设A（x1，），B（x2，），则有AE=x1﹣x2，BE=﹣，EC=﹣x2，ED=，
∴
=
， ∴
=
．
(2)、∵DM∥AE， ∴
， ∴A（m，n）则B（﹣
，﹣2n），
把A、B代入y=2x﹣2得到
， 解得
， ∴A（2，2），B（﹣1，﹣4），
由图象可知，
＞2x﹣2时，x＜﹣1或0＜x＜2．
(3)、由（2）可知反比例函数解析式为y=
，A（2，2），B（1，﹣4）， ∵四边形OBPQ是平行四边形，
∴OB=PQ，PO=BQ， ∵点B是定点，∴OB是定长， ∴要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可， ∵P在y=上，设P（a，
）， ∴OP2=n2+
=（n﹣
）2+8，
∴当n﹣
=0时，OP2的值最小， ∴n=±2时，OP有最小值， ∴P（2，2）或（﹣2，﹣2），Q（1，﹣2）或（﹣3，﹣6）．
